Math, math everywhere

给定 $N$ 的因式分解形式 $\prod_{i=1}^np_i^{\alpha_i}$ 和一个长为 $m$ 的字符串 $s$。 求 $k$ 的个数，使得 $0\leq k<N$ 且 $$\gcd(k+i,N)=1 \text{ if and only if }s_i=1$$ 模 $10^9+7$。 $m \leq 40$，$n\leq 5\times 10^5$，$p_i, \alpha_i \leq 10^9$。

If you have gone that far, you'll probably skip unnecessary legends anyway... You are given a binary string  and an integer 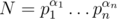. Find the number of integers $ k $ , $ 0<=k&lt;N $ , such that for all $ i=0 $ , $ 1 $ , ..., $ m-1 $ 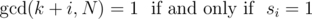 Print the answer modulo $ 10^{9}+7 $ .

In the first line of input there is a string $ s $ consisting of $ 0 $ 's and $ 1 $ 's ( $ 1<=|s|<=40 $ ). In the next line of input there is an integer $ n $ ( $ 1<=n<=5·10^{5} $ ). Each of the next $ n $ lines contains two space-separated integers $ p_{i} $ , $ α_{i} $ ( $ 1<=p_{i},α_{i}<=10^{9} $ , $ p_{i} $ is prime). All $ p_{i} $ are distinct.

A single integer — the answer to the problem.

1
2
2 1
3 1

2

01
2
3 2
5 1

15

1011
1
3 1000000000

411979884