CF814E An unavoidable detour for home

那些在长途旅行后不愿回家的人，将会受到蜗牛怪异的影响而迷失方向。怪异的携带者 Mayoi 并不希望这样的事情发生，但在找到解决方法之前，对此无能为力。现在，她只想知道，如果有人迷路了，将会面对多少种可能的情况。 在这个地区有 $n$ 个城镇，编号从 $1$ 到 $n$。编号为 $1$ 的城镇称为首都。交通网络由连通若干对城镇的双向道路组成。没有两条道路连接同一对城镇，也没有某条道路连接自身。每条道路所需的通行时间相同。迷路的旅行者无法分辨城镇之间的连接方式，但居民可以提供以下信息： - 从除了首都以外的每个城镇开始，通往首都的最短路径（即经过道路最少的路径）都存在且唯一； - 设 $l_{i}$ 表示从城镇 $i$ 到首都的最短路径所经过的道路数，则对于所有 $2 \leq i \leq n$ 都有 $l_{i} \geq l_{i-1}$； - 对于城镇 $i$，其连接的道路数用 $d_{i}$ 表示，$d_{i}$ 只能是 $2$ 或 $3$。 请你计算有多少种不同的方式可以连接这些城镇，并输出答案对 $10^9+7$ 取模。不同行的连通方式只要存在一对 $(u,v)$（$1 \leq u,v \leq n$），使得在一种方式中 $u$ 和 $v$ 之间有道路而另一种没有，就认为是不同的。

第一行输入一个正整数 $n$（$3 \leq n \leq 50$），表示城镇的数量。 第二行输入 $n$ 个用空格分隔的整数 $d_{1},d_{2},...,d_{n}$（$2 \leq d_{i} \leq 3$），分别表示 $1,2,...,n$ 号城镇连接的道路数。保证所有 $d_{i}$ 之和为偶数。

输出一个整数，表示满足条件的不同连通方式的总数，对 $10^9+7$ 取模。

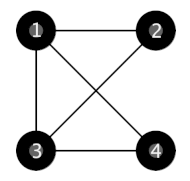
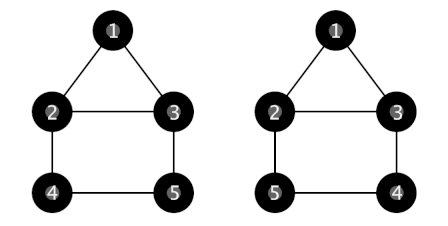
在第一个样例中，只有如下结构满足所有约束条件，城镇 $2,3,4$ 到首都的距离都是 $1$。  在第二个样例中，以下两种结构都满足约束条件。  由 ChatGPT 5 翻译