CF870E Points, Lines and Ready-made Titles

You are given $ n $ distinct points on a plane with integral coordinates. For each point you can either draw a vertical line through it, draw a horizontal line through it, or do nothing. You consider several coinciding straight lines as a single one. How many distinct pictures you can get? Print the answer modulo $ 10^{9}+7 $ .

N/A

N/A

In the first example there are two vertical and two horizontal lines passing through the points. You can get pictures with any subset of these lines. For example, you can get the picture containing all four lines in two ways (each segment represents a line containing it). The first way: 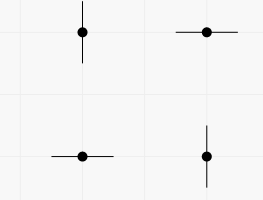 The second way: 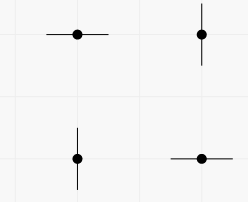In the second example you can work with two points independently. The number of pictures is $ 3^{2}=9 $ .