CF932D Tree
题目描述
## Tree
### 题目大意
需要维护一棵树,其中各点有其点权,要求支持 $q$ 次强制在线的操作:
1. 加入一个叶子;
2. 给出 $u, X$,查询满足下列条件的序列 $????[1 ⋯ t]$ 中的最大的 $t$:
- 要求 $s_1 = t$;
- 序列中所有节点的点权之和 $\le x$;
- 有 $s_i + 1$ 为 $s_i$ 的祖先,同时有 $s_i + 1$ 的点权不小于 $s_i$ 的点权,且树中 $s_i \to s_{i+1}$ 一段链上的节点(不含 $s_i, s_{i+1}$)点权均小于 $s_i$ 的点权。
给出一个权重为 $0$ 且索引为 $1$ 的树节点。设 $cnt$ 为该树中节点的数量(初始时,$cnt$ 被设为 $1$)。支持 $Q$ 个查询,查询分为以下两种类型:
- 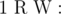 添加一个新节点(索引 `index` 为 $cnt + 1$)权重为 $W$,并在节点 $R$ 和此节点之间添加边;
- 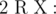 输出以 $R$ 为起始节点的节点序列的最大长度,该序列满足以下条件:
1. 以 $R$ 开始;
2. 序列中的每个节点都是其前驱的祖先;
3. 序列中节点的权重之和不超过 $X$;
4. 对于序列中连续的节点 $i,j$,如果 $i$ 是 $j$ 的祖先,则 $w[i] \geq w[j]$,且在从 $i$ 到 $j$ 的简单路径上不存在节点 $k$,使得 $w[k] \geq w[j]$。
树在任何时刻都以节点 $1$ 为根。
请注意,查询是以修改后的方式给出的。
输入格式
无
输出格式
无
说明/提示
在样例输入 1 中,$last=0$。
\- 查询 1: `1 1 1`,节点 $2$ (权重为 $1$)被添加到节点 $1$。
\- 查询 2: `2 2 0`,以 $2$ 为起始节点的节点序列中没有权重小于等于 $0$ 的节点。此时有 $last=0$ 。
\- 查询 3: `2 2 1`,答案是 $1$,序列为 $\{2\}$。此时有 $last=1$ 。
\- 查询 4: `1 2 1`,节点 $3$ (权重为 $1$)被添加到节点 $2$。
\- 查询 5: `2 3 1`,答案是 $1$,序列为 $\{3\}$。此处节点 $2$ 不能被添加,因为权重和不能大于 $1$。此时有 $last=1$ 。
\- 查询 6: `2 3 3`,答案是 $2$,序列为 $\{3,2\}$。此时有 $last=2$ 。
> 校对:Xue Ouyang & Emma Lee from MZES.