CF954C Matrix Walk

There is a matrix $ A $ of size $ x×y $ filled with integers. For every 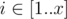, 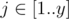 $ A_{i,j}=y(i-1)+j $ . Obviously, every integer from $ [1..xy] $ occurs exactly once in this matrix. You have traversed some path in this matrix. Your path can be described as a sequence of visited cells $ a_{1} $ , $ a_{2} $ , ..., $ a_{n} $ denoting that you started in the cell containing the number $ a_{1} $ , then moved to the cell with the number $ a_{2} $ , and so on. From the cell located in $ i $ -th line and $ j $ -th column (we denote this cell as $ (i,j) $ ) you can move into one of the following cells: 1. $ (i+1,j) $ — only if $ i<x $ ; 2. $ (i,j+1) $ — only if $ j<y $ ; 3. $ (i-1,j) $ — only if $ i>1 $ ; 4. $ (i,j-1) $ — only if $ j>1 $ . Notice that making a move requires you to go to an adjacent cell. It is not allowed to stay in the same cell. You don't know $ x $ and $ y $ exactly, but you have to find any possible values for these numbers such that you could start in the cell containing the integer $ a_{1} $ , then move to the cell containing $ a_{2} $ (in one step), then move to the cell containing $ a_{3} $ (also in one step) and so on. Can you choose $ x $ and $ y $ so that they don't contradict with your sequence of moves?

N/A

N/A

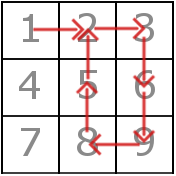The matrix and the path on it in the first test looks like this: Also there exist multiple correct answers for both the first and the third examples.