『SpOI - R1』架子鼓可以站 C

现在有一棵 $n$ 个点的树，树根是节点 $1$。 可以对这棵树做任意次**站 C 操作**，每次**站 C 操作**为：选择树上的一个叶子结点 $x$，再选择根节点到 $x$ 路径上的一条边，删除它；然后添加一条连接 $x$ 和根节点的边。 你需要求出经过若干次**站 C 操作**后树的直径的最大值。 **注意：叶子结点的定义是不为根节点，且度数为 $1$ 的节点。**

**本题包含多组测试。** 第一行一个整数 $T$，表示测试数据组数。 接下来 $T$ 组数据，每组第一行一个整数 $n$，第二行一个长为 $n-1$ 的序列 $f_i$，第 $i$ 项为 $i+1$ 号节点在树上的父亲。

对于每组数据，一行一个整数表示答案。

1
3
1 2

2

1
7
1 2 1 4 4 5

6

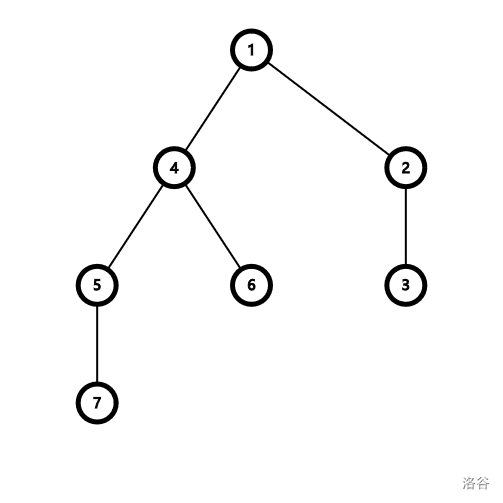
### 样例 #1 解释 不做操作时，树的直径为 $2$。可以证明这是最大的直径。 ### 样例 #2 解释 样例中的树如下：  只需要一次站 C 操作：选择叶子结点 $6$，断开 $1$ 到 $4$ 的边，再连接 $6$ 和 $1$。 这将会使树形成一条链，直径为 $6$。可以证明这是最大的直径。 ### 数据范围 **请注意常数因子对程序效率的影响。** **本题开启子任务捆绑与子任务依赖。** 对于所有数据，满足 $1\leq T\leq 10^4$，$2 \leq n \leq 2\times 10^5$，保证输入数据构成一棵树。 | Subtask | $T\leq$ | $n\leq$ | 特殊性质 | 得分 | 子任务依赖 | | :----------: | :----------: | :----------: | :----------: | :----------: | :----------: | | 1 | $10^4$ | $10$ | 无 | $15$ | 无 | | 2 | $10^4$ | $20$ | 无 | $15$ | 1 | | 3 | $10^4$ | $90$ | 无 | $20$ | 1,2 | | 4 | $10^4$ | $2\times 10^5$ | $A$ | $15$ | 无 | | 5 | $15$ | $2\times 10^5$ | 无 | $35$ | 1,2,3,4 | **特别地，对于 Subtask 4，保证 $\sum n\leq 3\times 10^6$。** 特殊性质 $A$：不存在一对 $x\neq 1\land y\neq 1$ 的 $(x,y)$ 满足 $\text{LCA}(x,y)=1$。