【MX-X8-T5】「TAOI-3」蓝宝石的存在证明

她背对着曾崇拜神的祭坛，就像在祈祷的圣女一样。 ——啊，神呀。这是何等的悲剧。 能否恳请您把这出悲剧变成喜剧，变成一出任何人也能开怀大笑的愉快喜剧? 然后，若是您大发慈悲，求求实现我的恋情。是的，唯有一回我也乐意。 向神发誓，我赌上一生来爱你。 向神发誓，我求得偿夙愿。

——只要打开这本魔法之书，自己的存在就会被世人遗忘。 世人之间的连接可以被看做一个 $n$ 个点的有标号无向简单**连通**图 $(V,E)$。此外，Kisaki 还会给你一个整数 $t \in \{0,1\}$，若 $t=0$，则这张无向连通图必须满足任意两点之间存在唯一的简单路径。若 $t=1$，则没有限制。 我们定义一个 $V$ 的一个子集 $W$ 是「紧密」的，当且仅当 $W$ 是图上的一个连通块，满足 $|W| \ge 2$，且对于任意 $u,v \in W$，都满足 $\text{dis}(u,v) \le 2$，其中 $\text{dis}(u,v)$ 为 $u,v$ 最短路径上的边数。 对于世人的一种连接方式，Kisaki 定义它是好的，当且仅当存在 **恰好** 一种方案把 $V$ 划分成若干点集，使得每个划分出的点集都是「紧密」的。 现在，Kisaki 告诉了你 $n$ 和 $t$，她想要知道，有多少种好的连接方式。当然，可能的方案是很多的，所以如你所想地——你所计算的方案数需要对模数 $P$ 取模（$P$ 未必是素数）。另外，她可能会问你很多次。

第一行，三个非负整数 $T, P, t$，其中 $T$ 为询问的次数。 接下来 $T$ 行，每行一个正整数 $n$。

$T$ 行，每行一个非负整数，代表询问的答案对 $P$ 取模的值。

8 998244353 1
1
2
3
5
98
197
1145
4950

0
1
4
65
369585723
752044625
87224156
664115047

8 998244353 0
1
2
3
5
98
197
1145
4950

0
1
3
65
607286080
653853011
777350973
422131392

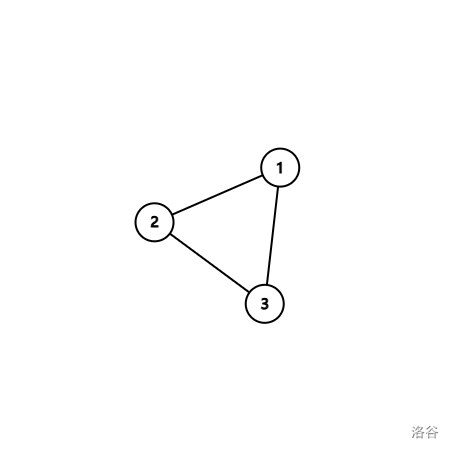
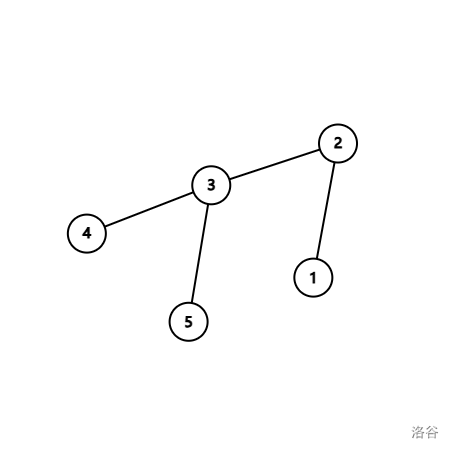
**【样例解释 #1】** 若 $n=3$ 且 $t=1$，一种合法的连接方式如图所示：  唯一一种对它的合法划分方案为，划分成 $\{1,2,3\}$ 这一个集合。这种连接方式在 $t=0$ 时是不合法的。 **【样例解释 #2】** 若 $n=5$，无论 $t=0$ 还是 $t=1$，一种合法的连接方式如图所示：  唯一一种对它的合法划分方案为，划分成 $\{1,2\}$ 和 $\{3,4,5\}$ 两个集合。 **【数据范围】** **本题采用捆绑测试。** - 子任务 1（1 分）：$P=1$。 - 子任务 2（6 分）：$n,T \le 7$，$t=0$。 - 子任务 3（6 分）：$n,T \le 7$，$t=1$。 - 子任务 4（12 分）：$P \le 2$，$t=1$。 - 子任务 5（23 分）：$t=0$。 - 子任务 6（21 分）：$n,T \le 100$。 - 子任务 7（17 分）：$P \ge 10^8$ 且 $P$ 为质数。 - 子任务 8（14 分）：无特殊限制。 对于所有数据，保证 $1 \le n,T \le 5 \times 10^3$，$0 \le t \le 1$，$1 \le P \le 1.05 \times 10^9$。