P11700 [ROIR 2025] 寻找宝藏

翻译自 [ROIR 2025 D1T4](https://neerc.ifmo.ru/school/archive/2024-2025/ru-olymp-regional-2025-day1.pdf)。

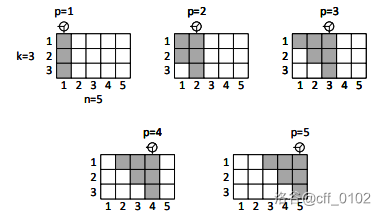
为了寻找有用的矿产资源，科学家们开发了一种特殊的扫描仪。 假设搜索区域是一个包含 $k$ 行和 $n$ 列的表格。行号从上到下编号为 $1$ 到 $k$，列号从左到右编号为 $1$ 到 $n$。每个单元格中可能含有矿产资源。 扫描仪的工作原理如下：它可以从第 $p$ 列启动，并返回扫描区域内包含矿产资源的单元格数。扫描区域包括第 $p$ 列的所有单元格、第 $p-1$ 列的前 $k-1$ 个单元格、第 $p-2$ 列的前 $k-2$ 个单元格，以此类推。下图展示了当 $k=3$，$n=5$ 时，所有可能的 $p$ 值的扫描区域。  现在，给定扫描仪返回的每个 $p$ 值的结果，记为 $b_p$，即在第 $p$ 列的扫描区域内，矿产资源的数量。如果一个表格的矿产资源分布能匹配扫描仪的返回值，则称这个表格是“合法的”。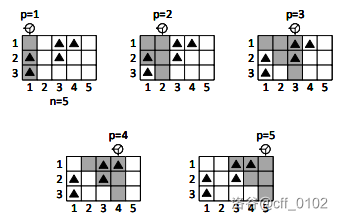比如，若扫描仪返回值为 $[2, 1, 2, 3, 2]$，则其中一个合法的表格可能如下所示（含有矿产的单元格用黑色三角形表示）：  你需要根据给定的扫描结果，确定合法表格的数量，并输出其对 $10^9 + 7$ 取模的结果。注意，扫描仪可能存在故障，导致没有任何合法的表格，这种情况下应输出 $0$。

无

无

本题使用 Subtask 捆绑测试。数据中 Subtask 0 是样例。 | 子任务 | 分数 | 特殊性质 | |:--------:|:------:|:----------:| | $1$ | $7 $ | $k \leq 2$ | 第一子任务 | | $2 $ | $9 $| $k \leq 3$ | 第一、二子任务 | | $3 $ | $9 $ | $k \leq 4$ | 第一、二、三子任务 | | $4 $ | $20 $ | $k \leq 5$ | 第一至四子任务 | | $5 $ | $15 $ | $k \leq 6$ | 第一至五子任务 | | $6 $ | $10 $ | $1 \leq n \cdot k \leq 25$ | 第一至五子任务 | | $7$ | $30$ | 无 | 第一至六子任务 |