P11724 [JOIG 2025] ポスター 2 / Poster 2

JOI 学院的理惠为三月举行的文化节制作了一张海报。海报可以视为一个 $N\times N$ 的网格；有 $K$ 种颜色，编号分别为 $1$ 到 $K$，每个格子的颜色是 $K$ 种颜色之一；具体地，网格的颜色可以用一个矩阵 $A$ 来表示：记第 $i$ 行第 $j$ 列的格子为 $(i,j)(1\le i,j\le N)$，那么 $(i,j)$ 的颜色为 $A_{i,j}(1\le A_{i,j}\le K)$。 学生希望海报的颜色可以丰富一点；他们定义一张海报的“鲜艳程度”为满足以下条件的 $(i,j)(1\le i,j\le N-1)$ 的个数： - $(i,j),(i+1,j),(i,j+1),(i+1,j+1)$ 中出现的颜色种类数不小于 $3$。 即 $A$ 中出现元素种类数不小于 $3$ 的 $2\times 2$ 子矩阵个数。 例如，下图中的海报的鲜艳程度为 $2$，因为存在 $2$ 个满足上述条件的 $2\times 2$ 子矩阵（已使用蓝框标出）。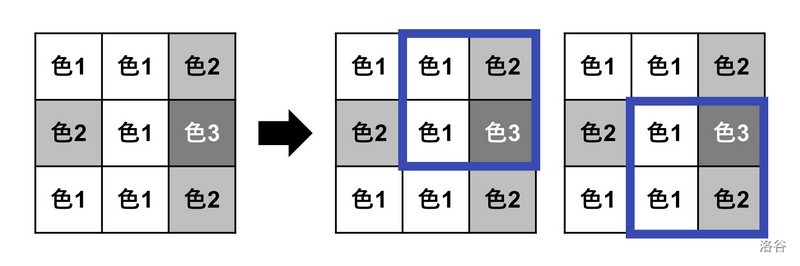  由于时间紧迫，学生们希望通过恰好**一次**以下操作，或者**不进行操作**，来最大化海报的鲜艳程度： - 选择**恰好一个**格子 $(i,j)$ 和一个与该格子原先颜色不同的颜色 $c(1\le c\le K)$，将格子 $(i,j)$ 的颜色改为 $c$，即 $A_{i,j}\gets c$。 请求出最终能得到的海报的最大鲜艳程度。

无

无

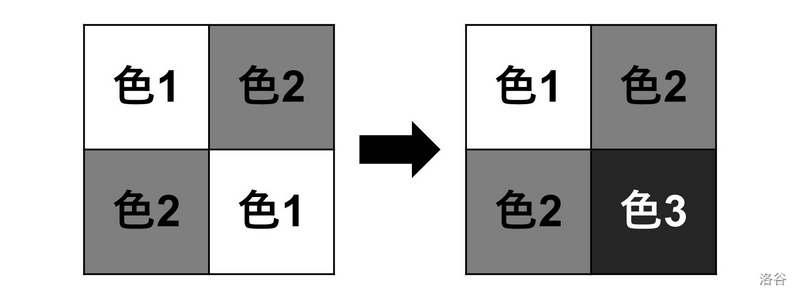
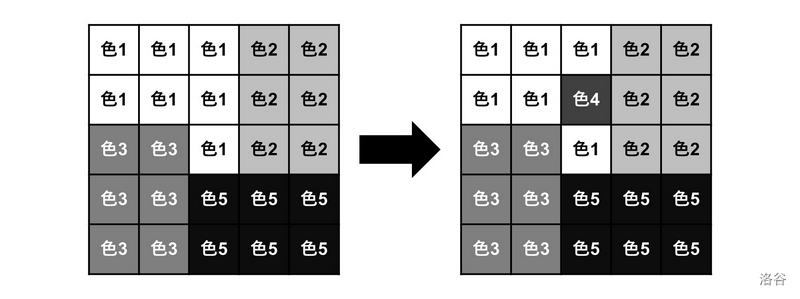
#### 【样例解释 #1】 如下图所示，将 $(2,2)$ 的颜色改为颜色 $3$，可以使得鲜艳程度为 $1$。  可以证明不存在更优的方案。 该样例满足子任务 $1,3,4,5$ 的限制。 #### 【样例解释 #2】 如下图所示，将 $(2,3)$ 的颜色改为颜色 $4$，可以使得鲜艳程度为 $5$。  可以证明不存在更优的方案。 该样例满足子任务 $3,4,5$ 的限制。 #### 【样例解释 #3】 该样例满足子任务 $2,4,5$ 的限制。 #### 【样例解释 #4】 该样例满足子任务 $3,4,5$ 的限制。 #### 【样例解释 #5】 该样例满足子任务 $4,5$ 的限制。 #### 【数据范围】 - $2\le N\le 270$； - $3\le K\le 10^9$； - $1\le A_{i,j}\le K(1\le i,j\le N)$。 #### 【子任务】 1. （$9$ 分）$N=2,K=3$； 2. （$6$ 分）$A_{i,j}(1\le i,j\le N)$ 两两不同； 3. （$27$ 分）$N,K\le 10$； 4. （$26$ 分）$N\le 10$； 5. （$32$ 分）无附加限制。