P11762 [IAMOI R1] Visiting Relatives

Xiao C took Xiao L to visit relatives.

Xiao C has $n$ relatives connected by $m$ bidirectional roads, ensuring all relatives are mutually reachable. Xiao C will personally visit them starting from the $s$-th relative's home. Each time she can move to a relative's home connected by a road. However, whenever she traverses a road, admirers swarm in causing congestion. She can choose to hide her charm (marking $p_i=1$) to prevent congestion, otherwise (marking $p_i=0$) the road becomes permanently blocked after this traversal. Xiao L is bad with directions, so Xiao C wants to leave exactly $n-1$ unblocked roads forming a connected tree, while traversing at most $k$ roads. Construct such a traversal plan. ### Formal Problem Statement Given a simple undirected connected graph with $n$ nodes and $m$ edges, construct a path satisfying: 1. Starts at node $s$ (end node unrestricted). 2. For each traversed edge $(u_i, v_i)$, assign $p_i \in \{0,1\}$ where: - $p_i=0$: Delete this edge (cannot be reused). - $p_i=1$: Keep this edge. - Path continuity: $u_i = v_{i-1}$ for $i>1$ (even if edge is deleted). 3. Path length ≤ $k$. 4. Remaining edges form a spanning tree. Multiple traversals allowed before deletion. Solution always exists under given constraints.

N/A

N/A

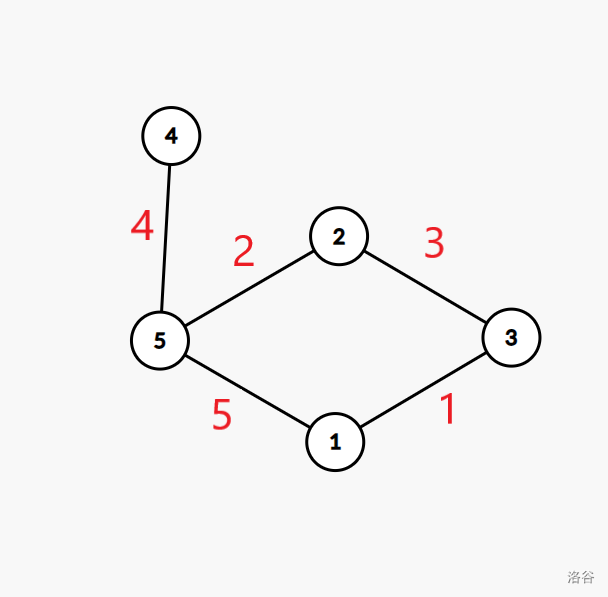
 After traversing edge 4 (keep) to node 5, then edge 2 (block), remaining edges form a tree. Alternative solutions like ``` 2 4 1 5 0 ``` or ``` 3 4 1 2 1 3 0 ``` are also valid. ### Constraints **Subtask scoring** | Subtask | $n \le$ | $m$ | $k=$ | Score | | :-----: | :-----: | :-----: | :-----: | :---: | | 1 | 10 | ≤10 | 100 | 20 | | 2 | 100 | ≤$\frac{n(n-1)}{2}$ | $10^6$ | 10 | | 3 | $10^3$ | $n$ | $n+m$ | 10 | | 4 | $10^3$ | ≤$\frac{n(n-1)}{2}$ | $n^2$ | 20 | | 5 | $10^3$ | ≤$\frac{n(n-1)}{2}$ | $n+m$ | 40 | For 100% data: - $n-1 \le m \le \frac{n(n-1)}{2}$ - No self-loops or duplicate edges Postscript: This is a modified version. The [original problem](https://www.luogu.com.cn/problem/T565042) remains unsolved. Contact [Down_syndrome](https://www.luogu.com.cn/user/984018) for ideas. Translation by DeepSeek R1