诸侯安置
题目描述
很久以前,有一个强大的帝国,它的国土成正方形状,如图所示。
这个国家有若干诸侯。由于这些诸侯都曾立下赫赫战功,国王准备给他们每人一块封地(正方形中的一格)。但是,这些诸侯又非常好战,当两个诸侯位于同一行或同一列时,他们就会开战。如下图为 $n=3$ 时的国土,阴影部分表示诸侯所处的位置。前两幅图中的诸侯可以互相攻击,第三幅则不可以。
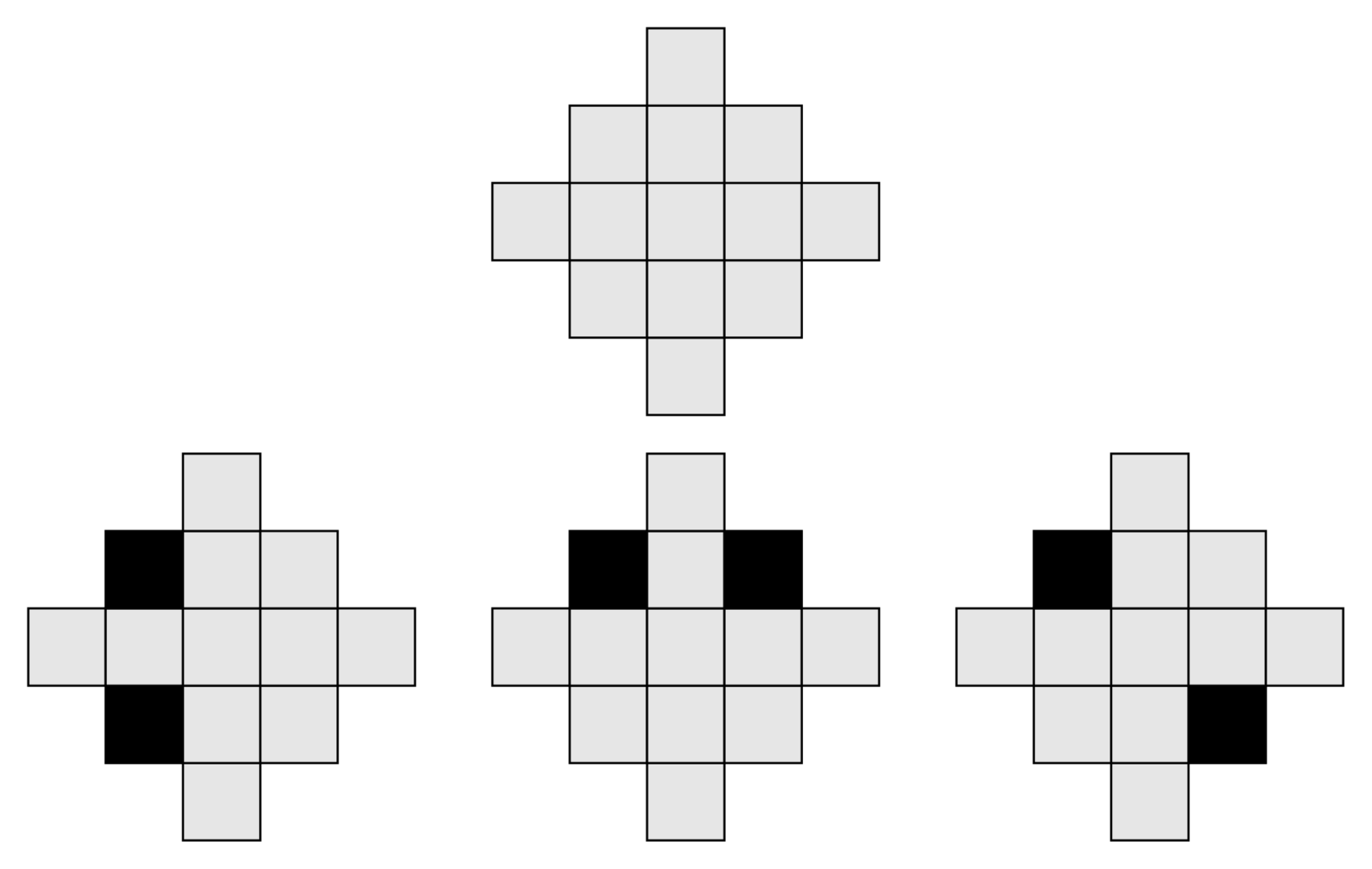
国王自然不愿意看到他的诸侯们互相开战,致使国家动荡不安。 因此,他希望通过合理的安排诸侯所处的位置,使他们两两之间都不能攻击。
现在,给出正方形的边长 $n$,以及需要封地的诸侯数量 $k$,要求你求出所有可能的安置方案数。(满足 $n\le100$,$k\le2n^2-2n+1$)
由于方案数可能很多,你只需要输出方案数除以 $504$ 的余数即可。
输入输出格式
输入格式
仅一行,两个整数 $n$ 和 $k$,中间用一空格隔开。
输出格式
一个整数,表示方案数除以 $504$ 的余数。
输入输出样例
输入样例 #1
2 2
输出样例 #1
4说明
注意:镜面和旋转的情况属于不同的方案。