显示图像

古老的显示屏是由 $N \times M$ 个像素（Pixel）点组成的。一个像素点的位置是根据所在行数和列数决定的。例如 $P(2,1)$ 表示第 $2$ 行第 $1$ 列的像素点。那时候，屏幕只能显示黑与白两种颜色，人们用二进制 $0$ 和 $1$ 来表示。$0$ 表示黑色，$1$ 表示白色。当计算机发出一个指令：$P(x,y)=1$，则屏幕上的第 $x$ 行第 $y$ 列的阴极射线管就开始工作，使该像素点显示白色，若 $P(x,y)=0$，则对应位置的阴极射线管不工作，像素点保持黑色。在某一单位时刻，计算机以 $N \times M$ 二维 $01$ 矩阵的方式发出显示整个屏幕图像的命令。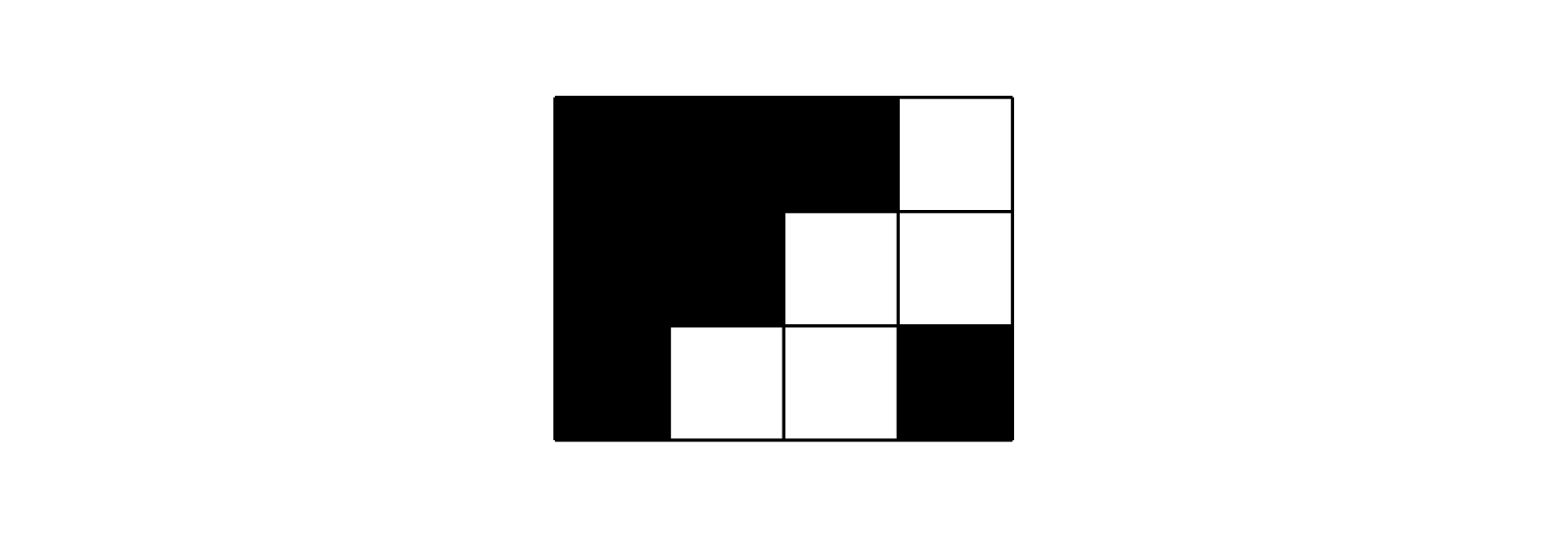 例如，屏幕是由 $3 \times 4$ 的像素点组成，在某单位时刻，计算机发出如下命令： $$\begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 \\ \end{pmatrix}$$ 对应屏幕显示应为：  假设放大后，一个格子表示一个像素点。 由于未知的原因，显示黑色的像素点总是受显示白色的像素点的影响——可能是阴极射线管工作的作用。并且，距离越近，影响越大。这里的距离定义如下： 设有像素点 $P_1(x_1,y_1)$ 和像素点 $P_2(x_2,y_2)$，则它们之间的距离 $D(P_1,P_2)=|x_1-x_2|+|y_1-y_2|$。 在某一时刻，计算机发出显示命令后，科学家们期望知道，每个像素点和其最近的显示白色的像素点之间的最短距离是多少——科学家们保证屏幕上至少有一个显示白色的像素点。 上面的例子中，像素 $P(1,1)$ 与最近的白色像素点之间的距离为 $3$，而像素 $P(3,2)$ 本身显示白色，所以最短距离为 $0$。

第一行有两个数字，$N$ 和 $M\ (1 \le N,M \le 182)$，表示屏幕的规格。 以下 $N$ 行，每行 $M$ 个数字，$0$ 或 $1$。为计算机发出的显示命令。

输出文件有 $N$ 行，每行 $M$ 个数字，中间用 $1$ 个空格分开。第 $i$ 行第 $j$ 列的数字表示距像素点 $P(i,j)$ 最近的白色像素点的最短距离。

3 4
0001
0011
0110

3 2 1 0
2 1 0 0
1 0 0 1

- 对于 $30\%$ 的数据：$N\times M \le 10000$； - 对于 $100\%$ 的数据：$N\times M \le 182^2$。