树的重量

树可以用来表示物种之间的进化关系。一棵“进化树”是一个带边权的树，其叶节点表示一个物种，两个叶节点之间的距离表示两个物种的差异。现在，一个重要的问题是，根据物种之间的距离，重构相应的“进化树”。 令 $N=\{1,2,3,\cdots ,n\}$，用一个 $N$ 上的矩阵 $M$ 来定义树 $T$。其中，矩阵 $M$ 满足：对于任意的 $i$，$j$，$k$，有 $M[i,j]+M[j,k] \ge M[i,k]$。树 $T$ 满足： 1. 叶节点属于集合 $N$； 2. 边权均为非负整数； 3. $d_T(i,j)=M[i,j]$，其中 $d_T(i,j)$ 表示树上 $i$ 到 $j$ 的最短路径长度。 如下图，矩阵 $M$ 描述了一棵树。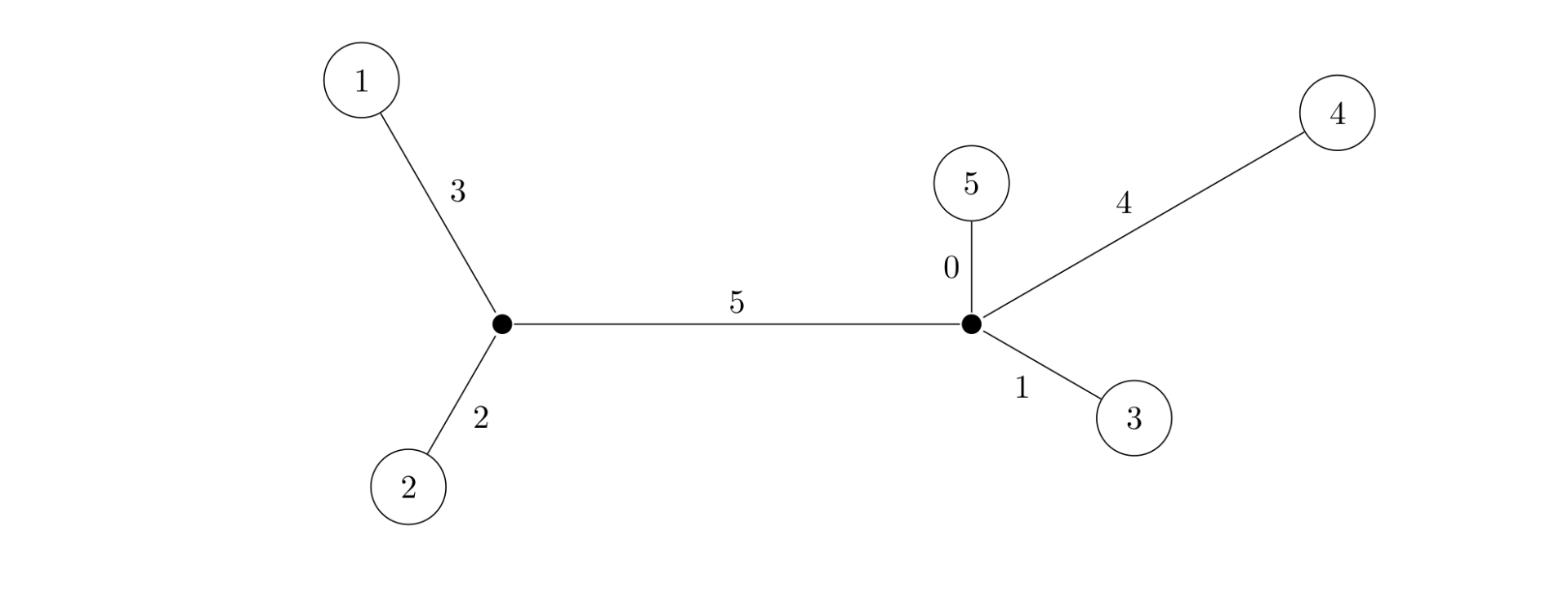 $$M=\begin{bmatrix} 0 & 5 & 9 & 12 & 8 \\ 5 & 0 & 8 & 11 & 7 \\ 9 & 8 & 0 & 5 & 1 \\ 12 & 11 & 5 & 0 & 4 \\ 8 & 7 & 1 & 4 & 0 \\ \end{bmatrix}$$ 树的重量是指树上所有边权之和。对于任意给出的合法矩阵 $M$，它所能表示树的重量是惟一确定的，不可能找到两棵不同重量的树，它们都符合矩阵 $M$。你的任务就是，根据给出的矩阵 $M$，计算 $M$ 所表示树的重量。下图是上面给出的矩阵 $M$ 所能表示的一棵树，这棵树的总重量为 $15$。 

第一行是一个整数 $n\ (2<n<30)$。 其后 $n-1$ 行，给出的是矩阵 $M$ 的一个上三角（不包含对角线），矩阵中所有元素是不超过 $100$ 的非负整数。输入数据保证合法。

对于每组输入，输出一行，一个整数，表示树的重量。

5
5 9 12 8
8 11 7
5 1
4

15

4
15 36 60
31 55
36

71