P1756 [NOI2009] 描边

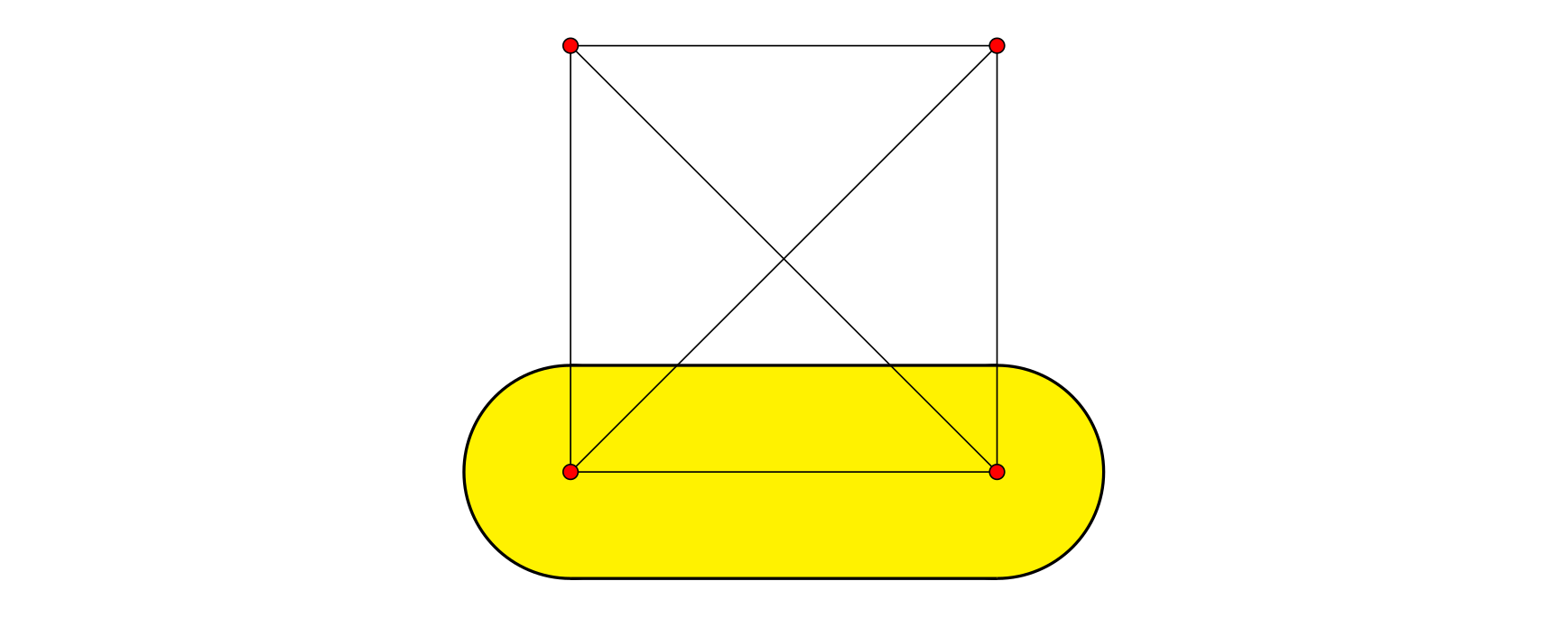
小 Z 是一位杰出的数学家。聪明的他特别喜欢研究一些数学小问题。 有一天，他在一张纸上选择了 $n$ 个点，并用铅笔将它们两两连接起来，构成 $\dfrac{n(n-1)}{2}$ 条线段。由于铅笔很细，可以认为这些线段的宽度为 $0$。 望着这些线段，小 Z 陷入了冥想中。他认为这些线段中的一部分比较重要，需要进行强调。因此小 Z 拿出了毛笔，将它们重新进行了描边。毛笔画在纸上，会形成一个半径为 $r$ 的圆。在对一条线段进行描边时，毛笔的中心（即圆心）将从线段的一个端点开始，沿着该线段描向另一个端点。下图即为在一张 $4$ 个点的图中，对其中一条线段进行描边强调后的情况。  现在，小 Z 非常想知道在描边之后纸面上共有多大面积的区域被强调，你能帮助他解答这个问题么？

无

无

每个测试点单独评分。 本题设有 $4$ 个评分参数 $p_1,p_2,p_3,p_4$（$p_1 \lt p_2 \lt p_3 \lt p_4$），已在输入文件中给出。 你的得分将按照如下规则给出： - 若你的答案与标准答案相差不超过 $p_1$，则该测试点你将得到满分； - 否则，若你的答案与标准答案相差不超过 $p_2$，则你将得到该测试点 $70\%$ 的分数； - 否则，若你的答案与标准答案相差不超过 $p_3$，则你将得到该测试点 $40\%$ 的分数； - 否则，若你的答案与标准答案相差不超过 $p_4$，则你将得到该测试点 $10\%$ 的分数； - 否则，该测试点你的得分为 $0$。