三角形图

请在 [这里](https://www.luogu.com.cn/paste/tre46v8i) 查看原题面。

UNowen 有 $n$ 个[平面向量](https://baike.baidu.com/item/%E5%B9%B3%E9%9D%A2%E5%90%91%E9%87%8F/448934?fr=ge_ala) $\{\bm L_n\}$，其中： - $|\bm L_1|=|\bm L_2|=\ldots=|\bm L_n|=1$； - $\bm L_1+\bm L_2+\ldots+\bm L_n=\bm 0$； - 对于任意正整数 $1 \le i,j \le n$，总存在整数 $k$ 使得 $\langle\bm L_i,\bm L_j\rangle=\dfrac{k\pi}{3}$；（[$\dfrac{k\pi}{3}=k \times 60^\circ$](https://baike.baidu.com/item/%E5%BC%A7%E5%BA%A6/1533188?fr=ge_ala)） - 除了整个向量序列以外（下同），向量序列中不存在和为 $\bm 0$ 的一段。 此处 $\langle\bm X,\bm Y\rangle$ 代指「将 $\bm X$ 旋转至与 $\bm Y$ 同向所旋转的角度」，逆时针为正角，顺时针为负角（例如，设 $\bm X=(\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2})$，$\bm Y=(1,0)$，则 $\langle\bm X,\bm Y\rangle=-\dfrac{\pi}{4}$）。 **也就是说，这 $n$ 个向量的长度（模）均为 $1$，并且首尾拼接可以得到一个封闭多边形。保证这个封闭多边形的各个内角均为 $\dfrac{\pi}{3}$ 的正整数倍，内部没有其他向量，并且不是空心的。** 为了表述方便，我们用一个长度为 $n$，字符集为 $\{\tt a,\tt b,\tt c,\tt d,\tt e,\#\}$ 的字符串 $S$ 来描述 $\{\bm L_n\}$。 具体地，对于 $S$ 的第 $i$ 个字符（特别地，$\bm L_0$ 等价于 $\bm L_n$，$\bm L_{n+1}$ 等价于 $\bm L_1$，下同）： | 字符 | 含义 | | :----------: | :----------: | | $\tt a$ | $\langle\bm L_i,\bm L_{i+1}\rangle=\dfrac{2\pi}{3}$ | | $\tt b$ | $\langle\bm L_i,\bm L_{i+1}\rangle=\dfrac{\pi}{3}$ | | $\tt c$ | $\langle\bm L_i,\bm L_{i+1}\rangle=0$ | | $\tt d$ | $\langle\bm L_i,\bm L_{i+1}\rangle=-\dfrac{\pi}{3}$ | | $\tt e$ | $\langle\bm L_i,\bm L_{i+1}\rangle=-\dfrac{2\pi}{3}$ | | $\tt \#$ | $\vert\langle\bm L_i,\bm L_{i+1}\rangle\vert=\pi$ |  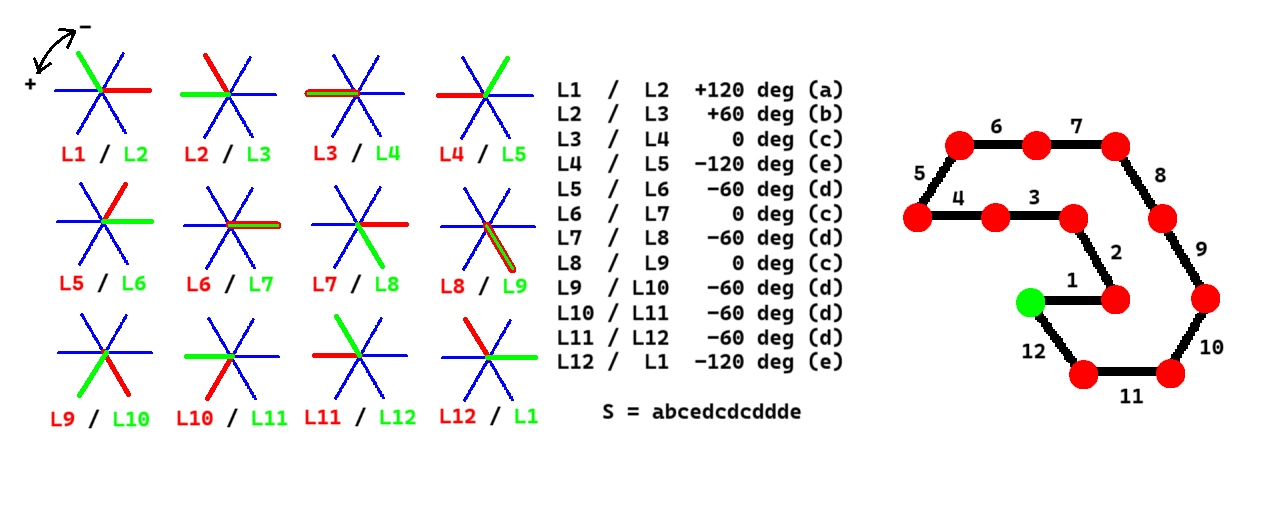此外，UNowen 按如下方式定义一个向量序列 $\{\bm L_1,\bm L_2,\ldots,\bm L_n\}$ 的「标准表示」： - 分别对于 $l=1,2,\ldots,n$，求出向量序列 $\{\bm L_l,\bm L_{l+1},\ldots,\bm L_n,\bm L_1,\bm L_2,\ldots,\bm L_{l-1}\}$ 对应的字符串： - 取 $n$ 个字符串中[字典序](https://baike.baidu.com/item/%E5%AD%97%E5%85%B8%E5%BA%8F/7786229?fr=ge_ala)最小的字符串作为向量序列 $\{\bm L_1,\bm L_2,\ldots,\bm L_n\}$ 的「标准表示」。 例如，上图中向量序列的「标准表示」是 $S=\texttt{abcedcdcddde}$，而不能是 $S=\texttt{dcdcdddeabce}$。 现在，UNowen 把向量序列 $\{\bm L_1,\bm L_2,\ldots,\bm L_n\}$ 对应的字符串 $S$（不一定是「标准表示」）给了你。他希望你可以按如下方式对这个向量序列进行一次修改： - 选定一个正整数 $1 \le k \le n$； - 构造两个平面向量 $\bm X,\bm Y$，使得： - $|\bm X|=1$； - $|\bm Y|=1$； - $\langle\bm L_k,\bm X\rangle=\dfrac{\pi}{3}$； - $\langle\bm L_k,\bm Y\rangle=-\dfrac{\pi}{3}$。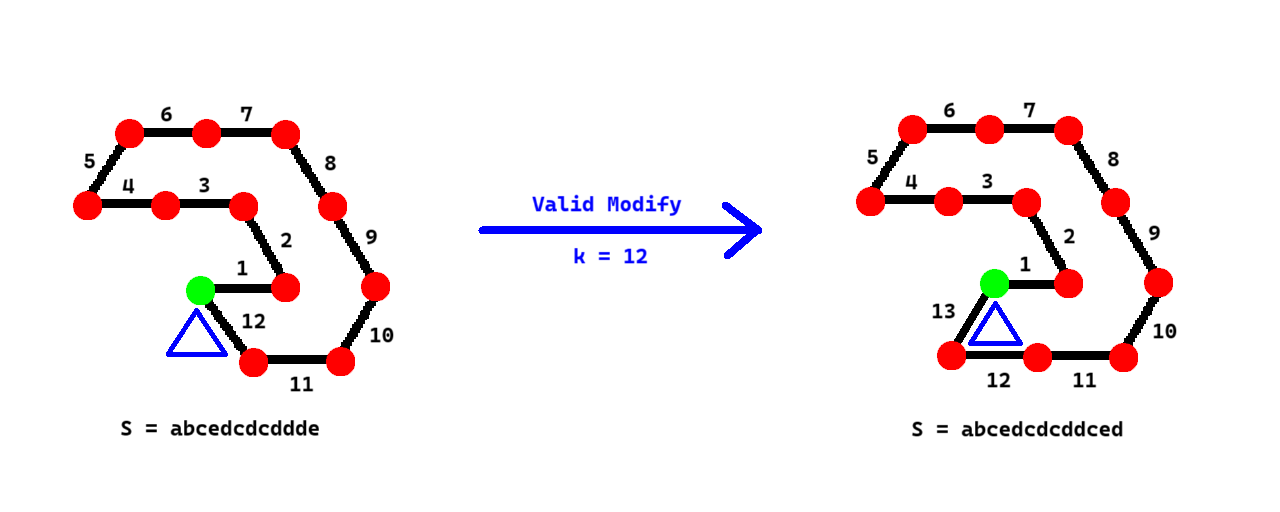 - 用 $\bm X,\bm Y$ 两项（$\bm X$ 在前，$\bm Y$ 在后）替换 $\bm L_k$； - 若 $\bm L_{k-1}+\bm X=\bm 0$，删除 $\bm L_{k-1},\bm X$； - 若 $\bm L_{k+1}+\bm Y=\bm 0$，删除 $\bm L_{k+1},\bm Y$； - 若修改后的向量序列中存在和为 $\bm 0$ 的一段（除了整个向量序列以外），那么 UNowen 称这次修改是不合法的。例如，在下面的图片中，如果选择 $k=3$，那么修改就是不合法的。 - UNowen 会将修改后的向量序列的「标准表示」定义为该次修改的「修改结果」。 - 对于任意两个修改方案，如果修改后的向量序列首尾拼接得到的图形全等，那么 UNowen 会认为这两个修改方案是等价的。例如，在下面的图片中，$k=1$ 和 $k=2$ 的两个修改方案就是等价的。 - **也就是说，修改操作会对封闭多边形上的某个向量向外作等边三角形，使得修改后的图形仍为满足上述要求（各个内角均为 $\dfrac{\pi}{3}$ 的正整数倍，内部没有其他向量，并且不是空心的）的封闭多边形。对于任意两个修改方案，如果修改后的向量序列首尾拼接得到的图形全等，那么它们是等价的。**  请求出互不等价的合法的修改方案的个数，并按字典序从小到大输出每个修改方案的「修改结果」。

**本题有多组数据。** 第一行一个正整数 $T$，表示数据组数。 下面 $T$ 行，每行一个字符集为 $\{\tt a,\tt b,\tt c,\tt d,\tt e\}$ 的非空字符串 $S$。保证 $\tt \#$ 不会出现。

对于每组数据，输出三行： 第一行一个正整数 $K$，表示，并按字典序从小到大输出每个修改方案。 第二行 $K$ 个字符集为 $\{\tt a,\tt b,\tt c,\tt d,\tt e\}$ 的非空字符串（用空格隔开），表示每个可能出现的「修改结果」。你需要按字典序从小到大的顺序输出它们。可以证明 $\tt \#$ 不会出现。 **第三行是空行。请特别注意这一点，因为它不符合传统题的一般数据格式。**

2
eee
cedde

1
dede

3
beddde cdecde cecece

2
adeccecced
dddddd

5
acedccecced addebcecced adebebecced adecbedcced cceccecce

1
cddddce

7
eee
cedde
adeccecced
dddddd
ccdeccde
baedddcdde
abcedcdcddde

1
dede

3
beddde cdecde cecece

5
acedccecced addebcecced adebebecced adecbedcced cceccecce

1
cddddce

4
bcdeccdde bcedccece bdeccdebe cccedccde

8
abdecdcddde abececcddde abedcebddde abeddbecdde abeddccecde abeddcdcece abeddcddced addddcdde

10
abbeddcdcddde abcdeccdcddde abcecebdcddde abcedbeccddde abcedccebddde abcedcdbecdde abcedcdccecde abcedcdcdcece abcedcdcddced acedcdcdddd

设 $|S|$ 为字符串 $S$ 的长度。 对于 $30\%$ 的数据，$T \le 5$，$|S| \le 9$。 对于 $50\%$ 的数据，保证所有的修改方案都是合法的。 对于 $100\%$ 的数据，$1 \le T \le 100$，$3 \le |S| \le 75$。