[SDOI2007] 立体分割

Ghy收了 $n$ 个小弟,如 Psf、Hf、Csr、Ll……也当然包括你啊。（原文如此……） 可是身为大哥的他从来不像小弟索要什么，反而经常给小弟分发礼物。 一天他得到了 $1$ 个长方体形状的蛋糕。但是Ghy并不喜欢吃蛋糕，所以他要把蛋糕全部分给小弟们。Ghy认为所有小弟是平等的，所以找来小弟你，让你把这个蛋糕分成 $n$个大小和形状都相等的长方体小蛋糕（即全等的小蛋糕）。 我们把蛋糕搬到一个三维坐标系里，以它的一个顶点 $O$ 为坐标原点 $(0,0,0)$。另一个与 $O$ 点相对的顶点(就是离 $O$ 点最远的点)的坐标 $(x,y,z)$。其实 $x,y,z$ 就表示了长方体的长、宽、高。

四个正整数，$x,y,z,n$。意义如题目所述。

$N$ 行，每行 $6$ 个实数，表示分割成的全等长方体小蛋糕的两相对顶点坐标，先输出第一个顶点的坐标 $x_1,y_1,z_1$，然后是 $x_2,y_2,z_2$，误差不超过 $10^{-9}$。（可以任意顺序输出小蛋糕坐标，且相对顶点任取一组输出）。

2 3 2 6

0 0 0 1 1 2
1 0 0 2 1 2
0 1 0 1 3 1
0 1 1 1 3 2
1 1 0 2 3 1
1 1 1 2 3 2

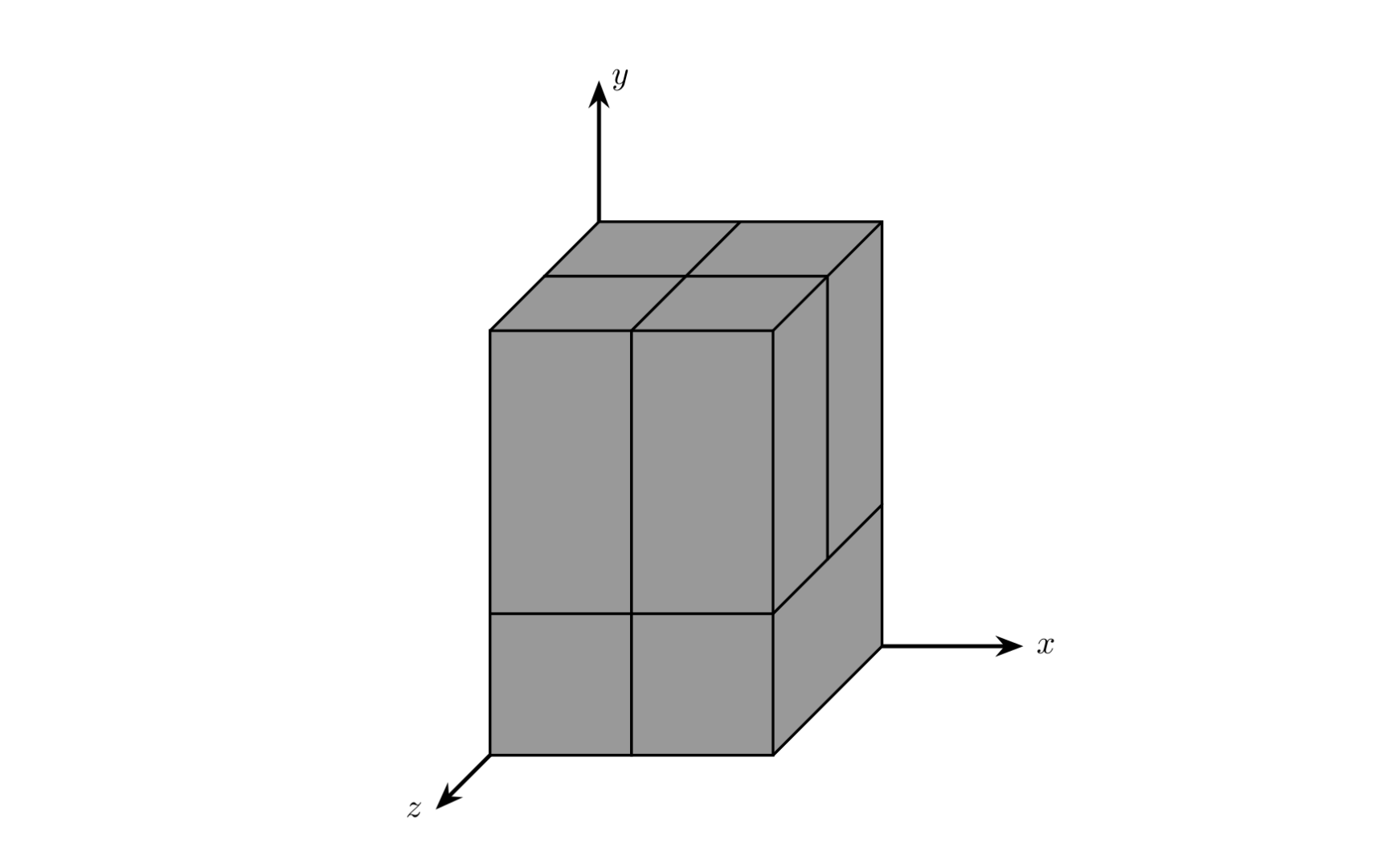
### 样例解释（2023.9.29 管理员补充）  ### 数据范围及约定 对于 $100\%$ 的数据，$1\leq x,y,z,n\leq 1000$，$x,y,z$ 为整数。