P2674 《瞿葩的数字游戏》T2-多边形数
题目背景
数字王国里有一类特殊的数,它们叫做多边形数。并且国王 $1$ 规定数字间的联姻只能在同为一种多边形数中进行。(请不要吐槽这个规定……)
瞿葩对这个现象十分好奇,见 $36$ 和 $10$ 这一对情侣在散步,便上前询问 $36$ 它是什么多边形数。可是 $36$ 拍拍脑门,想了想说:“我也不知道啊,你去问问国王吧。”
看来国民们并不知道自己是什么多边形数啊,国王 $1$ 急的发愁。国王 $1$ 只知道多边形数怎么计算,但是多边形数要怎么给国民做解释呢,干脆这样解释吧:可以排成正多边形的整数都是多边形数。当然多边形数可以分为三边(角)形数、四边形数(正方形数)、五边形数、六边形数……
题目描述
**此题为规律题,请自行寻找规律,以锻炼数学归纳能力!!**
我们拿三角形数做例子:图中的 $1$、$3$、$6$、$10$ 就是三角形数。
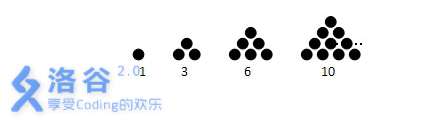
任务:求出 $N$ 是哪一种多边形数(假设 $N$ 是 $K$ 边形数),比如我们求出 $36$ 是三边形数和四边形数(貌似叫做三角形数和正方形数呵)。若不是多边形数,输出 Poor + 该数字。若同时是多种多边形数,输出最小的一个和第二小的一个。每个读入文件里有 $ng$ 组数据。
输入格式
无
输出格式
无
说明/提示
### 数据范围及约定
对于 $20\%$ 的数据,$1 \le K_1,K_2 \le 6$;
对于 $100\%$ 的数据, $1 \le N \le 10^6$,$1 \le ng \le 10^2$。
如果同时是多种多边形数,设 $K_1$ 为最小的 $K$,$K_2$ 为次小的 $K$。
国王 $1$:“你可以发现四边形数(正方形数)就是平方数这个规律吗?为方便理解,我给出前几个多边形数表。”(表中可以看出,正六边形不包括正中心的那个点,以此类推)
| 自然数 | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ |
| :-: | :-: | :-: | :-: | :-: | :-: | :-: | :-: | :-: |
| 三角形数 | $1$ | $3$ | $6$ | $10$ | $15$ | $21$ | $28$ | $36$ |
| 正方形数 | $1$ | $4$ | $9$ | $16$ | $25$ | $36$ | $49$ | $64$ |
| 五边形数 | $1$ | $5$ | $12$ | $22$ | $35$ | $51$ | $70$ | $92$ |
| 六边形数 | $1$ | $6$ | $15$ | $28$ | $45$ | $66$ | $91$ | $120$ |