[ZJOI2013] 蚂蚁寻路

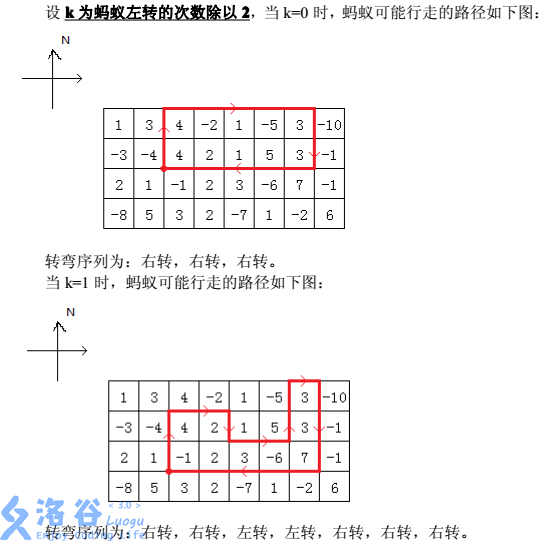
在一个 $n \times m$ 的棋盘上，每个格子有一个权值，初始时，在某个格子的顶点处一只面朝北的蚂蚁，我们只知道它的行走路线是如何转弯，却不知道每次转弯前走了多长。 蚂蚁转弯是有一定特点的，即它的转弯序列一定是如下的形式：右转，右转，左转，左转，右转，右转…左转，左转，右转，右转，右转。即两次右转和两次左转交替出现的形式，最后两次右转（最后两次一定是右转）后再多加一次右转。我们还知道，蚂蚁不会在同一个位置连续旋转两次，并且蚂蚁行走的路径除了起点以外，不会到达同一个点多次，它最后一定是回到起点然后结束自己的行程，而且蚂蚁只会在棋盘格子的顶点处转弯。  现在已知棋盘大小、每个格子的权值以及左转次数除以 $2$ 的值，问蚂蚁走出的路径围出的封闭图形，权值之和最大可能是多少。

第一行三个数 $n,m,k$。意义如题目描述。 接下来一个 $n$ 行 $m$ 列的整数矩阵，表示棋盘。

一个数，表示蚂蚁所走路径围出的图形可能的最大权值和。

2 5 2
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1

-8

### 样例说明 除了第一行的第二个和第一行的第四个都要围起来才至少合法。 ### 数据规模与约定 - $10\%$ 的数据所有格子中权值均非负。 - 另 $20\%$ 的数据 $n=2$。 - 另 $30\%$ 的数据 $k=0$。 - $100\%$ 的数据 $1 \le n\le 100$，$1 \le m \le 100$，$0 \le k \le 10$，保证存在合法路径，数据有梯度，格子中每个元素的值绝对值不超过 $10000$。