[POI2011] WYK-Plot

### 题目描述 **译自 POI 2011 Round 1. E「[Plot](https://szkopul.edu.pl/problemset/problem/mzrTn1kzVBOAwVYn55LUeAai/site/?key=statement)」** 给定 $n$ 个点 $ \left( P_1, \ldots, P_n \right) $，将其分成不多于 $m$ 个连续的段： $$ \left( P_{k_0 + 1}, \ldots, P_{k_1} \right), \left( P_{k_1 + 1}, \ldots, P_{k_2} \right), \ldots, \left( P_{k_{s - 1}+ 1}, \ldots, P_{k_s} \right), $$ 其中 $ 0 = k_0 \lt k_1 \lt k_2 \lt \ldots \lt k_s = n $，且对于 $ i = 1, \ldots, s $，子序列 $ \left( P_{k_{i - 1}+ 1}, \ldots, P_{k_i} \right) $ 用一个新点 $Q_i$ 替代。这时我们说 $ P_{k_i - 1}, \ldots, P_{k_i} $ 这些点被「收缩」到了点 $Q_i$，从而产生一个新的点集 $ Q_1, \ldots, Q_s $。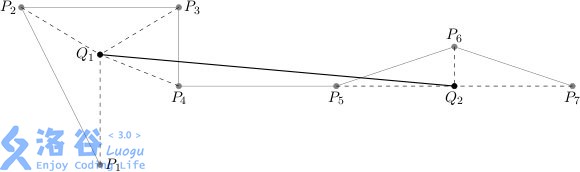两个点集的相似度定义为 $ P_1, \ldots, P_n $ 这些点与其对应的「收缩」后的点距离的最大值： $$ \max_{i = 1, \ldots, s} \left( \max_{j = k_{i-1}+1, \ldots, k_i}\left( d\left( P_j, Q_i \right) \right) \right) ,$$ 其中 $ d\left( P_j, Q_i \right) $ 表示 $P_j$ 和 $Q_i$ 之间的距离，公式为： $$ d \left( \left(x_1, y_1 \right), \left( x_2, y_2 \right) \right) = \sqrt{ \left( x_2 - x_1 \right)^2 + \left( y_2 - y_1 \right)^2 } $$  上图为一个将 $ (P_1, \ldots, P_7) $ 收缩为 $ ( Q_1, Q_2 ) $ 的例子，其中 $ (P_1, \ldots, P_4) $ 被收缩为 $ Q_1 $，$ (P_5, P_6, P_7) $ 被收缩为 $Q_2$. 给定 $n$ 个点组成的序列，你需要将其「收缩」为最多 $m$ 个点，使得相似度最小。原序列可以任意切割。受限于浮点数的精度限制，只要答案比最优解多出不超过 $ 0.000001$ 即算正确。 ### 输入格式 第一行两个整数 $n$ 和 $m$，$ 1 \le m \le n \le 100000 $，用一个空格分开。 接下来 $n$ 行每行两个整数，用一个空格分开。第 $i+1$ 行两个整数 $x_i, y_i$（$ -1000000 \le x_i,y_i \le 1000000$），表示 $P_i$ 的坐标为 $(x_i, y_i)$. ### 输出格式 第一行一个实数 $d$，表示与原序列的相似度。 接下来一个整数 $s$，表示收缩后点集的大小。 接下来 $s$ 行表示 $Q_i, \ldots, Q_s$ 的坐标。每行两个整数 $u_i$ 和 $v_i$ 表示 $Q_i$ 的坐标 $ (u_i, v_i) $。 翻译来自于 [LibreOJ](https://loj.ac/p/2159)。

We call any sequence of points in the plane a plot. We intend to replace a given plot $(P_1,\cdots,P_n)$ with another that will have at most $m$ points ($m\le n$) in such a way that it "resembles" the original plot best. The new plot is created as follows. The sequence of points $P_1,\cdots,P_n$ can be partitioned into $s$ ($s\le m$) contiguous subsequences: $(P_{k_0+1},\cdots,P_{k_1}),(P_{k_1+1},\cdots,P_{k_2}),\cdots,(P_{k_{s-1}+1},\cdots,P_{k_s})$ where $0=k_0<k_1<k_2<\cdots<k_s=n$,and afterwards each subsequence $(P_{k_{i-1}+1},\cdots,P_{k_i})$, for $i=1,\cdots,s$,is replaced by a new point $Q_i$. In that case we say that each of the points $P_{k_{i-1}+1},\cdots,P_{k_i}$ has been contracted to the point $Q_i$. As a result a new plot, represented by the points $Q_1,\cdots,Q_s$, is created. The measure of such plot's resemblance to the original is the maximum distance of all the points $P_1,\cdots,P_n$ to the point it has been contracted to: $max_{i=1,\cdots,s}(max_{j=k_{i-1}+1,\cdots,k_i}(d(P_j,Q_i)))$ where $d(P_j,Q_i)$ denotes the distance between $P_j$ and $Q_i$, given by the well-known formula: $d((x_1,y_1),(x_2,y_2))=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$  An exemplary plot $P_1,\cdots,P_7$ and the new plot $(Q_1,Q_2)$, where $(P_1,\cdots,P_4)$ are contracted to $Q_1$, whereas $(P_5,P_6,P_7)$ to $Q_2$. For a given plot consisting of $n$ points, you are to find the plot that resembles it most while having at most $m$ points, where the partitioning into contiguous subsequences is arbitrary. Due to limited precision of floating point operations, a result is deemed correct if its resemblance to the given plot is larger than the optimum resemblance by at most $0.000001$.

In the first line of the standard input there are two integers $n$ and $m$, $1\le m\le n\le 100\ 000$, separated by a single space. Each of the following $n$ lines holds two integers, separated by a single space. The $(i+1)$-th line gives $x_i$,$y_i$,$-1\ 000\ 000\le x_i,y_i\le 1\ 000\ 000$ denoting the coordinates $(x_i,y_i)$ of the point $P_i$.

In the first line of the standard output one real number $d$ should be printed out, the resemblance measure of the plot found to the original one. In the second line of the standard output there should be another integer $s$, $1\le s\le m$. Next, the following $s$ lines should specify the coordinates of the points $Q_1,\cdots,Q_s$,one point per line. Thus the $(i+2)$-th line should give two real numbers $u_i$ and $v_i$, separated by a single space, that denote the coordinates $(u_i,v_i)$ of the point $Q_i$.All the real numbers should be printed with at most 15 digits after the decimal point.

7 2
2 0
0 4
4 4
4 2
8 2
11 3
14 2

3.00000000
2
2.00000000 1.76393202
11.00000000 1.99998199