P3521 [POI 2011] ROT-Tree Rotations

给定一颗有 $n$ 个**叶节点**的二叉树。每个叶节点都有一个权值 $p_i$（注意，根不是叶节点），所有叶节点的权值构成了一个 $1 \sim n$ 的排列。 对于这棵二叉树的任何一个结点，保证其要么是叶节点，要么左右两个孩子都存在。 现在你可以任选一些节点，交换这些节点的左右子树。 在最终的树上，按照先序遍历遍历整棵树并依次写下遇到的叶结点的权值构成一个长度为 $n$ 的排列，你需要最小化这个排列的逆序对数。

无

无

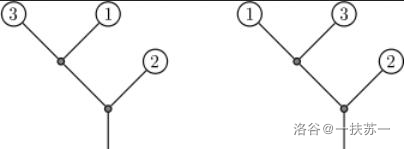
### 样例 1 解释 下图中，左图是初始读入的树，右图是操作后的树。  ### 数据规模与约定 - 对于 $30\%$ 的数据，保证 $n \leq 5 \times 10^3$。 - 对于 $100\%$ 的数据，保证 $2 \leq n \leq 2 \times 10^5$， $0 \leq x \leq n$，所有叶节点的权值是一个 $1 \sim n$ 的排列。 ### 提示 请注意，$n$ **不是**树的结点个数。