[TJOI2008] 小偷
题目背景
一位著名的小偷进入了一个充满宝石的储藏室,这个储藏室是由一连串房间构成的,房间的标号从 $0$ 开始,想进入第 $i$ 个房间就必须从第 $i-1$ 个房间进入,如图:
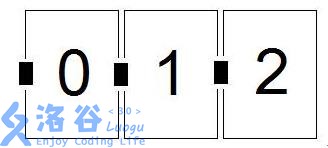
题目描述
上图为三个房间的情况,黑色的部分为连通两个房间的门,从左向右的编号分别为 $0,1,2\cdots$。已知当小偷从第 $0$ 个门进入储藏室时,储藏室的计时系统开始计时,每个门都有自己的关闭时间。每个屋里有不同种类的宝石,对于每种宝石,它的价值和小偷拿走它所耗费的时间也是不同的,为了简化问题,我们设想小偷在各个屋子之间走动的时间可以忽略不计,而且所有屋子里各种宝石的数量都是无限多的,那么请问小偷在能成功逃出来的情况下,可能获得宝石的最大价值。
附:对于每扇门,小偷都必须在严格早于此门关闭的时候出来才可以。
输入输出格式
输入格式
每组测试数据的第一行有两个整数 $N$ 和 $M$,分别代表储藏室有 $N$ 个房间,并且有 $M$ 种宝石。第二行中会有 $N$ 个正整数,分别表示第 $i$ 个门关闭的时间(门的编号从 $0$ 开始),接下来的 $M$ 行,每行有三个整数 $r,v$ 和 $t$,分别代表这种宝石所在的房间编号为 $r$,它的价值为 $v$,小偷拿走它所耗费的时间为 $t$。
输出格式
输出小偷在成功逃出储藏室的情况下获得宝石的最大价值。
输入输出样例
输入样例 #1
3 4
9 5 5
0 1 2
1 2 2
2 3 2
2 5 3
输出样例 #1
8说明
### 样例解释
虽然在第 $2$ 个房间中价值为 $5$ 的宝石好,但是不如拿两次价值为 $3$ 的宝石,在拿两次第 $0$ 房间中价值为 $1$ 的宝石,总价值为 $8$。
### 数据范围及约定
对于 $100\%$ 的数据,储藏室的屋子数量不超过 $50$,每扇门关闭的时间不超过 $1000$,并且宝石的数量不超过 $100$,价值不超过 $1000$。