P4224 [清华集训 2017] 简单数据结构
题目描述
参加完IOI2018之后就是姚班面试。而你，由于讨厌物理、并且想成为乔布斯一样的创业家，被成功踢回贵系。
转眼，时间的指针被指向2019，大二，12月初，考试周。
你早听学长说，数据结构期中考很难，对竞赛生不友好，集训队选手做不完卷子。
你冷笑。哼，堂堂国际金，这点难度的考试算什么。
两小时，你看完习题解析前五章所有内容，并且倒背如流；
一小时，你看了500页的讲义，并且记忆犹新；
十分钟，你骑车到考场，自信的你只带了一把水笔，虽然考试让带资料；
现在，摊开传说中神级卷子，你定神一看——
给出一个长度为 $N$ 的序列 $A_1,A_2,\cdots,A_N$，如果 $A$ 中的一个子序列 $B_1,B_2,\cdots,B_M$，满足条件：
$1 \le M \le N$
∀$1 \le i \le M$，$B_i$|$B_{i+1}$
那么称 $B$ 为 $A$ 的上升倍数子序列。
现在有一个长度为 $N$ 的序列 $A$ 被初始化为 $A_{1},A_{2},\cdots,A_{N}$，以及 $Q$ 次对序列 $A$ 的操作。此处要求实现如下四种操作：
0 x：在序列 $A$ 的最左端插入一个数字 $x$；
1 x：在序列 $A$ 的最右端插入一个数字 $x$；
2：移除序列 $A$ 最左端的一个数字；
3：移除序列 $A$ 最右端的一个数字；
在初始化序列 $A$ 和每次操作之后，请计算此时序列 $A$ 中最长上升倍数子序列的长度 $\mathrm{MaxLen}$，以及所有长度为 $\mathrm{MaxLen}$ 的上升倍数子序列的不同的开头数 $\mathrm{Cnt}$，输出 $\mathrm{MaxLen}$ 和 $\mathrm{Cnt}$。
为了大幅度降低题目难度，保证在任意时刻序列 $A$ 非空，其中的元素互不相等，并且均为 $1\sim M$ 之间的正整数；同一个数字最多只会被插入 $C$ 次。
输入格式
无
输出格式
无
说明/提示
**样例解释**
表格中以//隔开不同开头的最长上升子序列。
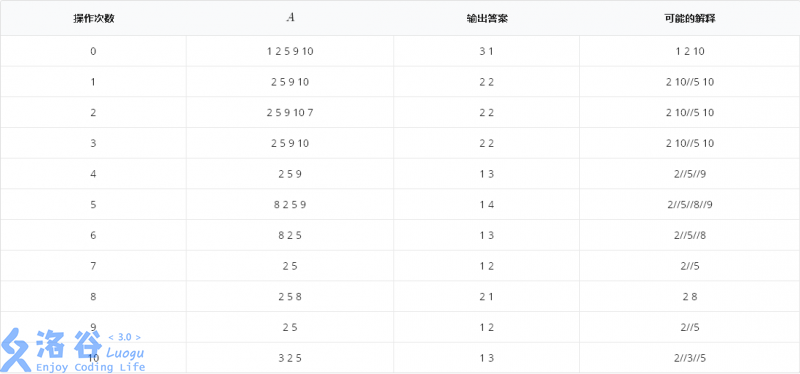
对于所有的数据，有 $1\le N \le 10^5$，$N\le M \le 10^6$，$0\le Q \le 10^5$，$1\le A_i\le M$，$C=10$。
下表展示了某些数据点的一些特殊约束，其中只有1表示只有形如1 x的操作，其他表述同理。
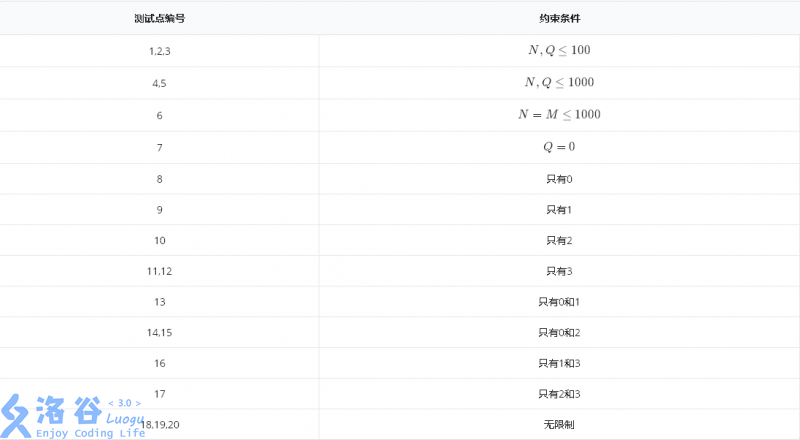
后记
“奋战两小时，考个四五十”的表情包占领了你的朋友圈：
“啊，感觉自己人生完全了”
“但愿……我真的能拿到四五十”
“我考完了……考完了……完了”
“曾经以为是开玩笑的，原来我还是naïve了”
你冷笑。提前半小时交卷，你自然觉得，数据结构，满分，正常。