[Code+#4] Tommy 的结合
题目背景
深邃的天空仿佛要吞噬一切,一场 Codeforces 比赛刚刚结束。“怎么还不理我……”,睡眼惺忪的 Tommy 拿起盖在一旁的手机。空空荡荡的 QQ 提示框,没有一丝的温度。Tommy 叹了口气。昏黄的灯发出微弱的光芒,抚摸着呼呼作响的电脑。
桌面上堆满了写满 $\partial$ 和 $\int$ 的草稿纸,手机闪光灯自制的简易台灯发出刺眼的白光;灯火缱绻,映照一双如画倦容。十几个 DDL 就在附近,QQ 那边的人已经三天三夜没有合眼了。这是 Tommy 所不知道的事。
题目描述
人生大概就是这样。在这物欲横流的红尘紫陌中,芸芸众生为了生计四处奔走,交谈越来越少,感情越来越淡。但是,著名科学家 Access Globe 的最新研究成果可以解决这样的问题:通过增加同时做的事情来增加共同语言。
A 和 B 都得到了一些任务,设他们要执行的任务集合分别为 $V_A$ 和 $V_B$。对每个人来说,任务 $1$ 是必须一开始做的,而其他的每个任务 $e$ 都存在一个前置任务 $p_e$,表示任务 $e$ 必须在任务 $p_e$ 完成后才能执行。也就是说,每个人的任务的依赖关系构成了一棵**有根外向树**,一个任务 $e$ 能被执行当且仅当 $p_e,p_{p_{e}},\cdots,1$ 这些任务全部都被执行,称 $p$ **依赖**任务 $p_e,p_{p_{e}},\cdots,1$。
现在,A 和 B 希望他们能有一些任务是共同完成的,因此他们决定这样选出一些任务:A 选出 $m$ 个任务 $a_1,\cdots,a_m$,要求 $a_1=1$,并且对于任意的 $1\le i<m$,都要求 $a_{i+1}$ 依赖任务$a_i$,同时 B 也选出 $m$ 个满足同样要求的任务 $b_1,\cdots,b_m$,这样,A 就可以沿着从 $1$ 到 $A_m$ 的路径依次执行这些任务,同时 B 也可以沿着 $1$ 到 $B_m$ 的路径依次执行这些任务;并且经过安排,当 A 在执行任务 $a_i$ 的时候,B 恰好在执行任务 $b_i$,在这时 A 和 B 就能取得联系,增进感情。
模型的目标为最大化亲密度。对于一组同时执行任务的关系 $a_i$ 和 $b_i$,可以获得 $C_{a_i,b_i}$ 的得分;同时,A 和 B 一旦失去联系,就会使得亲密度降低,在每一分钟,如果一方距离上次和对方联系后已经执行任务 $i$ 分钟,就会使得亲密度降低 $2i-1$。
例如,两个人要做的任务所花费的时间分别为 $2,1,4,7$ 和 $4,8,3,6,4$,并且共同完成了第一个任务和最后一个任务,那么 A 在执行中间两个任务的 $1+4=5$ 分钟没有和 B 联系,使得亲密度降低 $1+3+...+11=25$;同时 B 在执行中间三个任务的 $8+3+6=17$ 分钟没有和 A 联系,使得亲密度降低 $1+3+...+35=289$。注意,亲密度的计算只和任务执行的时间有关;并且任意两个任务都可以作为 $a_i$ 和 $b_i$ 同时执行,不需要保证它们花费的时间相同。
现在,给出 A 和 B 的任务、依赖关系和每个任务的执行时间,请你帮我们求出能够获得的最大的亲密度。
输入输出格式
输入格式
从标准输入读入数据。
第一行两个整数 $|V_A|,|V_B|$;
第二行 $|V_A|-1$ 个整数 $t^{(a)}_{2},t^{(a)}_{3},...,t^{(a)}_{|V_A|}$,表示 A 的每个任务的时间长度;
第三行 $|V_B|-1$ 个整数 $t^{(b)}_{2},t^{(b)}_{3},...,t^{(b)}_{|V_B|}$,表示 B 的每个任务的时间长度;
第四行 $|V_A|-1∣$ 个整数 $p^{(a)}_{2},p^{(a)}_{3},...,p^{(a)}_{|V_A|}$,表示 A 的每个任务的前置任务,保证 $p^{(a)}_{i}< i$;
第五行 $|V_B|-1$ 个整数 $p^{(b)}_{2},p^{(b)}_{3},...,p^{(b)}_{|V_B|}$,表示 B 的每个任务的前置任务,保证 $p^{(b)}_{i}< i$;
接下来 $|V_A|-1$ 行,每行 $|V_B|-1$ 个整数,第 $i-1$ 行第 $j-1$ 列为 $C_{i,j}$,表示 A 和 B 同时分别执行对应的任务 $i,j$ 能获得的亲密度,注意这些亲密度不一定是非负的;
注意以上输入均不包括第 1 个任务的信息,因为它和亲密度的计算没有关系。
输出格式
输出到标准输出。
输出能获得的最大的亲密度。
输入输出样例
输入样例 #1
5 4
2 1 2 1
1 1 1
1 2 3 4
1 2 2
-8 -1 6
4 -3 7
-7 5 5
-7 5 -5输出样例 #1
5说明
**样例解释**
A 和 B 分别选出任务 $1,3,4$ 和 $1,2,3$,同时执行的任务对 $(1,1)$、$(3,2)$ 和 $(4,3)$ 使得他们获得了 $4+5=9$ 的亲密度;A 孤独地执行任务 $2$ 的 $2$ 分钟丢失了 $1+3=4$ 的亲密度,因此最终的总亲密度为 $9-4=5$。这就是亲密度最大的方案。
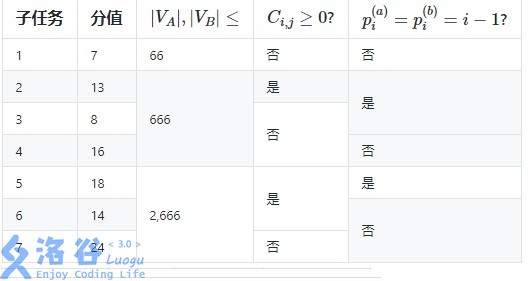
对于所有数据,$2\le |V_A|,|V_B|\le 2,666$,$1\le t^{(a)}_i,t^{(b)}_i\le 1,206$,$0\le |C_{i,j}|\le 2,017,011,328$。
Credit: https://www.luogu.org/discuss/show/38908
Credit:idea 与命题/陈俊锟 验题/Tommy > <
Git Repo:https://git.thusaac.org/publish/CodePlus4
感谢腾讯公司对此次比赛的支持。