[八省联考 2018] 劈配

一年一度的综艺节目《中国新代码》又开始了。Zayid 从小就梦想成为一名程序员，他觉得这是一个展示自己的舞台，于是他毫不犹豫地报名了。

轻车熟路的 Zayid 顺利地通过了海选，接下来的环节是导师盲选，这一阶段的规则是这样的： 总共 $n$ 名参赛选手（编号从 $1$ 至 $n$ ）每人写出一份代码并介绍自己的梦想。接着 由所有导师对这些选手进行排名。为了避免后续的麻烦，规定**不存在排名并列的情况**。 同时，每名选手都将独立地填写一份志愿表，来对总共 $m$ 位导师（编号从 $1$ 至 $m$ ）作出评价。志愿表上包含了共 $m$ 档志愿。对于每一档志愿，选手被允许填写最多 $C$ 位导师，每位导师最多被每位选手填写**一次**（**放弃某些导师也是被允许的**）。 在双方的工作都完成后，进行录取工作。每位导师都有自己战队的人数上限，这意味着可能有部分选手的较高志愿、甚至是全部志愿无法得到满足。节目组对“前 $i$ 名的录取结果最优”作出如下定义： - 前 $1$ 名的录取结果最优，**当且仅当**第 $1$ 名被其最高非空志愿录取（**特别地**，如果第 $1$ 名没有填写志愿表，那么该选手出局）。 - 前 $i$ 名的录取结果最优，当且仅当在前 $i - 1$ 名的录取结果最优的情况下，第 $i$ 名 被其理论可能的最高志愿录取（特别地，如果第 $i$ 名没有填写志愿表，或其所有志愿中的导师战队均已满员，那么该选手出局）。 如果一种方案满足“前 $n$ 名的录取结果最优”，那么我们可以简称这种方案是**最优的**。 举例而言，$2$ 位导师 $\rm T$ 老师、 $\rm F$ 老师的战队人数上限分别都是 $1$ 人；$2$ 位选手 Zayid 、DuckD 分列第 $1$ 、 $2$ 名。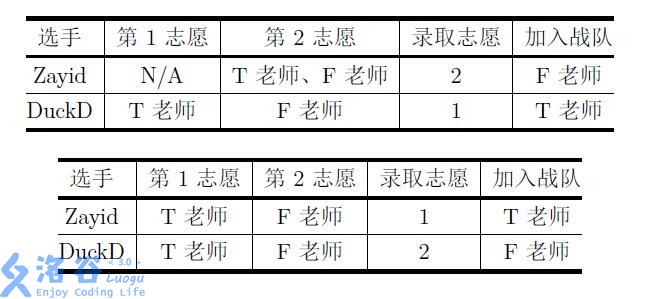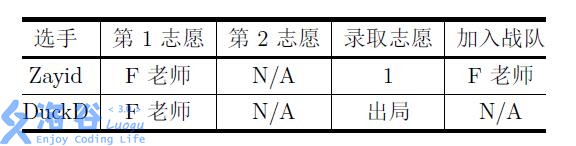那么下面 $3$ 种志愿表及其对应的最优录取结果如表中所示：   可以证明，对于上面的志愿表，对应的方案都是唯一的最优录取结果。 每个人都有一个自己的理想值 $s_i$ ，表示第 $i$ 位同学希望自己被第 $s_i$ 或更高的志愿录取，如果没有，那么他就会非常沮丧。 现在，所有选手的志愿表和排名都已公示。巧合的是，每位选手的排名都恰好与它们的编号相同。 对于每一位选手，Zayid 都想知道下面两个问题的答案： - 在最优的录取方案中，他会被第几志愿录取。 - 在其他选手相对排名不变的情况下，至少上升多少名才能使得他不沮丧。 作为《中国新代码》的实力派代码手，Zayid 当然轻松地解决了这个问题。不过他还是想请你再算一遍，来检验自己计算的正确性。

每个测试点包含多组测试数据，第一行 $2$ 个用空格隔开的非负整数 $T,C$ ，分别表示数据组数、每档志愿最多允许填写的导师数目。 接下来依次描述每组数据，对于每组数据： - 第 $1$ 行两个用空格隔开的正整数 $n,m$ 。 > $n,m$ 分别表示选手的数量、导师的数量。 - 第 $2$ 行 $m$ 个用空格隔开的正整数：其中第 $i$ 个整数为 $b_i$ 。 > $b_i$ 表示编号为 $i$ 的导师战队人数的上限。 第 $3$ 行至第 $n + 2$ 行，每行 $m$ 个用空格隔开的非负整数：其中第 $i + 2$ 行左起第 $j$ 个数为 $a_{i,j}$ 。 > $a_{i,j}$ 表示编号为 $i$ 的选手将编号为 $j$ 的导师编排在了第 $a_{i,j}$ 志愿。特别地，如果 $a_{i,j}= 0$ ，则表示该选手没有将该导师填入志愿表。 > 在这一部分，保证每行中不存在某一个正数出现超过 $C$ 次（ **$0$ 可能出现超过 $C$ 次**），同时保证所有 $a_{i,j} \leqslant m$ 。 - 第 $n + 3$ 行 $n$ 个用空格隔开的正整数，其中第 $i$ 个整数为 $s_i$ 。 > $s_i$ 表示编号为 $i$ 的选手的理想值。 > 在这一部分，保证 $s_i \leqslant m$ 。

按顺序输出每组数据的答案。对于每组数据，输出 $2$ 行： - 第 $1$ 行输出 $n$ 个用空格隔开的正整数，其中第 $i$ 个整数的意义为： 在最优的录取方案中，编号为 $i$ 的选手会被该档志愿录取。 > **特别地，如果该选手出局，则这个数为 $m + 1$** 。 - 第 $2$ 行输出 $n$ 个用空格隔开的非负整数，其中第 $i$ 个整数的意义为： 使编号为 $i$ 的选手不沮丧，最少需要让他上升的排名数。 > **特别地，如果该选手一定会沮丧，则这个数为 $i$ 。**

3 5
2 2
1 1
2 2
1 2
1 1
2 2
1 1
1 2
1 2
2 1
2 2
1 1
0 1
0 1
2 2

2 1
1 0
1 2
0 1
1 3
0 1

1 5
4 3
2 1 1
3 1 3
0 0 1
3 1 2
2 3 1
2 3 3 3

1 1 3 2
0 0 0 0

- 样例 $1$ 解释 三组数据分别与【题目描述】中的三个表格对应。 对于第 $1$ 组数据：由于选手 $1$ 没有填写第一志愿，所以他一定无法被第一志愿录取，也就一定会沮丧。选手 $2$ 按原排名就不沮丧，因此他不需要提升排名。 对于第 $2$ 组和第 $3$ 组数据： $1$ 号选手都不需要提升排名。而希望被第一志愿录取的 $2$ 号选手都必须升到第 $1$ 名才能如愿。 - 样例 $2$ 解释 $1$ 号选手的第一志愿只填写了 $2$ 号导师，因此 $1$ 号选手必定被 $2$ 号导师录取。 $2$ 号选手的第一志愿只填写了 $3$ 号导师，因此 $2$ 号选手必定被 $3$ 号导师录取。 由于 $2,3$ 号导师均满员，且 $3,4$ 号选手均填写了 $1$ 号导师，因此他们都会被 $1$ 号导师录取。 所以 $1,2$ 号选手均被第 $1$ 志愿录取，$3$ 号选手被第 $3$ 志愿录取， $4$ 号选手被第 $2$ 志愿录取。 由于他们都如愿以偿了，所以他们都不需要提升名次。 |测试点编号|$n \leqslant$|$m \leqslant$|$C$|其他约定| |:----:|:---:|:----:|:----:|:----:| |1| $10$|$1$|$=1$|无| |2|$10$|$2$|$=2$|$s_i=m$| |3|$10$|$3$|$=3$|无| |4|$100$|$100$|$=1$|$b_i=1$| |5|$100$|$100$|$=1$|无| |6|$200$|$200$|$=1$|$b_i=1$| |7|$200$|$200$|$=1$|无| |8|$100$|$100$|$=10$|无| |9|$200$|$200$|$=10$|$b_i=1$| |10|$200$|$200$|$=10$|无| - 对于所有测试点，保证 $ T \leqslant 5$ 。 - 对于所有测试点钟的所有数据，保证 $ m \leqslant n \leqslant 200, b_i \leqslant n$