[BJWC2018] 拓扑序列

小 C 最近学习了拓扑排序的相关知识。对一个有向无环图 $G$ 进行拓扑排序，是将 $G$ 中所有顶点排成一个线性序列，使得对图 $G$ 中任意一条有向边 $(u,v)$，$u$ 在线性序列中出现在 $v$ 之前。例如，如果图 $G$ 的点集为 $\{1,2,3,4\}$，边集为 $\{(1,2) ,(1,3),(2,4),(3,4)\}$，那么 $(1,2,3,4)$ 和 $(1,3,2,4)$ 都是图 $G$ 的拓扑序列。 现在小 C 对一个简单（无重边）有向无环图进行了拓扑排序，但不小心把原图弄丢了。除了拓扑序列，小 C 只记得原图的边数为 $k$，而且图中存在一个顶点 $u$ 可以到达其他所有顶点。他想知道有多少个满足上述要求的简单有向无环图。由于答案可能很大，你只需要输出答案模 $m$ 的余数。

输入第一行包含三个整数 $n,k,m$。 第二行是空格隔开的 $n$ 个正整数 $a_1,a_2,…,a_n$，表示原图的一个拓扑序列，保证是 $1$ 到 $n$ 的一个排列。

仅输出一个整数， 表示满足要求的简单有向无环图个数模 $m$ 的余数。

4 4 4
1 2 3 4

1

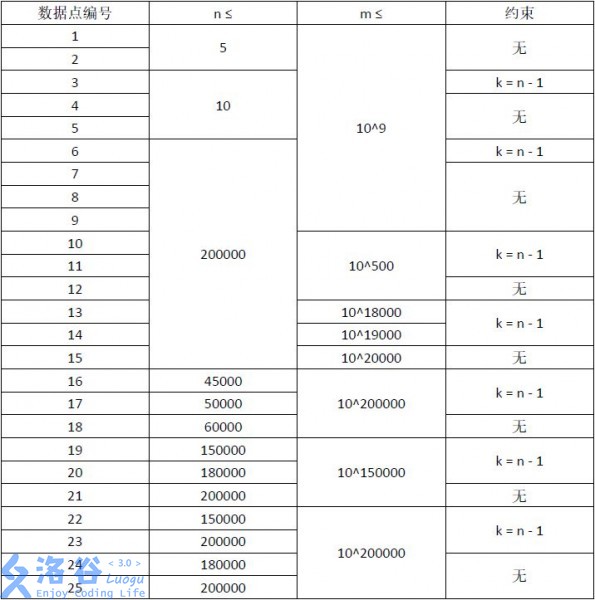
**【样例说明】** 共有 $9$ 个满足要求的简单有向无环图，边集分别为： $\{(1, 2), (1, 3), (1, 4), (2, 3)\}$ $\{(1, 2), (1, 3), (1, 4), (2, 4)\}$ $\{(1, 2), (1, 3), (1, 4), (3, 4)\}$ $\{(1, 2), (1, 3), (2, 3), (2, 4)\}$ $\{(1, 2), (1, 3), (2, 3), (3, 4)\}$ $\{(1, 2), (1, 3), (2, 4), (3, 4)\}$ $\{(1, 2), (1, 4), (2, 3), (2, 4)\}$ $\{(1, 2), (1, 4), (2, 3), (3, 4)\}$ $\{(1, 2), (2, 3), (2, 4), (3, 4)\}$ **【数据规模和约定】** 对于 $100\%$ 的数据 ，$0 \le k \le n \le 2\times 10^5$，$1 \leq m \leq 10^{200000}$。