[CTSC2005] 合并正方形

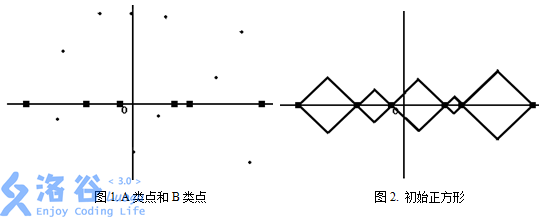
一个二维平面初始时为空，有一串往平面中加入点的命令。 加入的点有两种，这里称为 A 类点和 B 类点（如图 1，黑色正方形表示 A 类点，小圆黑点表示 B 类点）。A 类点一定位于 $X$ 轴上，而且不会重叠，而 B 类点可以出现在平面上的任何一个位置，可以重叠。每个 B 类点有一个权值 $W$。  处理：一、最初，将相邻两个 A 类点之间连一个与 $X$ 轴成 $45$ 度的正方形（如图 2）。二、每次可以将任意两个有公共点的正方形合并为一个大正方形，合并之后两个小正方形消失。图 2 的左数第 $2$、$3$ 的正方形合并后在图 3 中表示为灰边正方形。  合并后的正方形将平面划分为 $9$ 个区域，与正方形 $4$ 条边相邻的 $4$ 个区域分别为图 3 中的 I，II，III，IV。落在区域 I 中的 B 类点的权值和记为 $w_1$，落在区域 II 中的 B 类点的权值和记为 $w_2$，落在区域 III 中的 B 类点的权值和记为 $w_3$，落在区域 IV 中的 B 类点的权值和记为 $w_4$。落在灰色正方形内部的 B 类点的权值和记为 $w_5$（B 类点保证不会出现在任何一个区域的边界上），则合并费用为 $w_1+2w_2+3w_3+4w_4+5w_5$。落在其他区域的 B 类点不予考虑。每次合并之后并不影响 B 类点在平面上的位置和它自己所拥有的权值。 每进行一次合并，由 A 类点形成的正方形会减少一个，直到只剩下一个正方形为止。合并总费用为每次合并费用之和。不同合并顺序的合并费用可能会不同。 点是一个一个加入到平面的。加入第 $i$ 个 A 类点后，平面上有 $i$ 个 A 类点和在此之前加入的所有 B 类点。设此时的**最小**合并费用为 $f(i)$。 给定费用限制 $L$，编程求出 A 类点的最大数目 $K$，使得**前 $K$ 个 A 类点**的最小合并费用不超过 $L$，即 $f(K)\le L$。

第一行包含两个数 $M$，$L$，表示有 $M$ 条加入点的命令，费用限制为 $L$。 以下包含 $M$ 行，每行一个字母表示点的类型。`A` 表示 A 类点，`B` 表示 B 类点。对于 A 类点，后面一个数表示这个点的 $X$ 坐标；对于 B 类点，后面三个数表示这个点的 $X$，$Y$ 坐标和这个点的权值。

输出文件仅包含一个整数 $K_{max}$，即使 $f(K) \le L$的最大 $K$。

8 30.0
A -2
A 0
B 7 8 5.0
B 4 -3 2.0
B -3 4 1.0
A 2
B -4 5 1.0
A 4

3

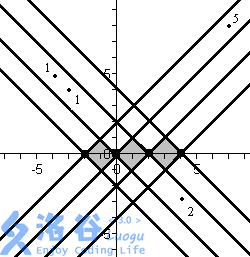
### 样例说明 输入最后一个点时，所有点如下图。B 类点旁边的数字为权值。  合并前 $3$ 个点的最小费用为 $f(3) = 27$，合并前 $4$ 个点的最小费用 $f(4) = 36$。由于 $f(3) < 30$ 而 $f(4) > 30$，因此最大的 $K$ 为 $3$。 ### 约定 $3 \le \text{A 类点的数目} \le 30000$ $5 \le M \le 100000$ $X$，$Y$均为整数，绝对值不超过 $10000000$ $L, W$ 均为实数，$0<W \le 10000$，$L\le 10^{11}$，所有输入实数最多保留三位小数 $50\%$ 的数据满足 $M \le3000$