P4558 [JSOI2018] 机器人

九条可怜是一个懒懒的女孩子。因为懒得扫地，九条可怜买了一架扫地机器人。 九条可怜的家可以抽象成一个 $n \times m$ 的网格，坐标从 $(1,1)$ 到 $(n,m)$ 。每一天晚上，可怜都会在 $(1,1)$ 处启动扫地机器人。在启动了之后，扫地机器人会按照设定好的路径开始行动，当再一次回到 $(1,1)$ 后便会停止。 因为一些技术原因，扫地机器人只能向右（列编号加一）或者向下（行编号加一）走。为了让扫地机器人能够顺利的回到 $(1,1)$ ，可怜在家中安装了一些通道，使得： 1. 如果机器人目前在 $(i,m)$ ，那么向右走一步会到 $(i,1)$ 。 2. 如果机器人目前在 $(n,i)$ ，那么向下走一步回到 $(1,i)$ 。 可怜希望，在启动了机器人之后，在机器人回到 $(1,1)$ 前，它可以经过每一个格子**恰好**一次。这样既可以把家里给打扫干净，也不会花太多时间。经过简单的计算，可怜很快就得到了所有不同的方案（两个方案是不同的当且仅当他们经过格子的顺序不同）。于是可怜把所有的方案都输入到了扫地机器人里。 这一天可怜购置了一些新的家具，放好家具之后，家里便多了一些扫地机器人无法通过的障碍，于是在所有之前准备的方案中，扫地机器人都会撞上某一个障碍而停止工作。 对于一个方案 $S$，可怜定义 $f(S)$ 为在这个方案中，扫地机器人在撞上障碍之前，经过了多少个格子。现在可怜想要对所有不同的方案，计算 $f(S)$ 的和。

无

无

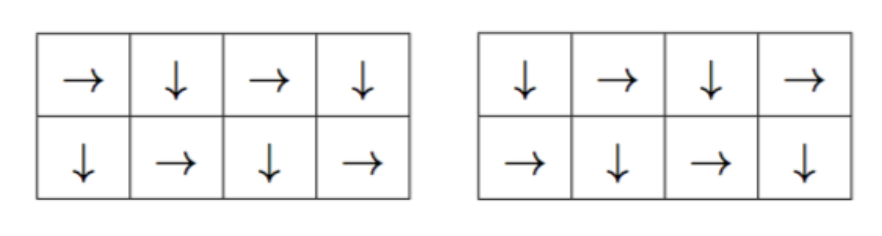
**样例 1 解释** $n=2,m=4$ 时，一共有两种合法的方案：  在第一种方案中,机器人在撞上障碍 $(1,3)$ 之前，一共经过了 $4$ 个格子。 在第二种方案中,机器人在撞上障碍 $(2,1)$ 之前，一共经过了 $1$ 个格子。 因此第二组测试数据的答案为 $1+4=5$ 。 **数据范围** 测试数据 1 $(20\%)$: $n,m\le 4$ 。 测试数据 2 $(30\%)$: $n,m\le 50$ ，且除了 $(1,1)$ 外所有格子都是障碍。 测试数据 3 $(50\%)$: $n,m\le 50$ 。 对于所有测试数据，$T\le 10;n,m\ge 1$ 。