孤舟蓑笠翁

 出于保护鱼类的目的，最优秀的渔翁才能在洞庭湖继续捕鱼。经过层层选拔，洞庭湖上只剩下孤舟蓑笠翁。以前跟其他渔翁一起钓鱼、打牌、切磋武艺，而如今只剩孤单一人，蓑笠翁不禁黯然神伤。选拔被淘汰，如今他们都去哪里了呢？大概回家种田养猪了吧。

 蓑笠翁现在闲暇时在练的武术名为"左右互搏术"，相传是周伯通首创的武功。 练功时，蓑笠翁的双手在某竖直平面内运动，以该平面上某点作为坐标原点，向右为 $x$ 轴正方向，向上为 $y$ 轴正方向建立直角坐标系。那么该平面内的一个点就可以用坐标 $(x, y)$ 来表示。 该武功有 $n$ 个可停顿点，分别为 $p_1 = (x_1, y_1), p_2 = (x_2, y_2), \ldots, p_n = (x_n, y_n)$。我们可以将蓑笠翁练功的过程分成一秒一秒来看，第 $i$ 秒时，双手都处于可停顿点上。而第 $i$ 秒末双手进行移动，移动到其它可停顿点上。（当然也可以不移动） 左右互搏术中，有 $k$ 种绝招。第 $i$ 种绝招为：左手处于 $v_i$ 号可停顿点，右手处于 $u_i$ 号可停顿点，则可以发动绝招。 练武功也有禁忌，在两只手停顿的时候，如果两只手的曼哈顿距离小于 $d_{min}$，则容易走火入魔。如果两只手的曼哈顿距离大于 $d_{max}$，则蓑笠翁的胳膊显然快被扯断了。所以假设左手在 $l$ 号停顿点，右手在 $r$ 号停顿点，则需要满足 $d_{min} \leq |x_l - x_r| + |y_l - y_r| \leq d_{max}$。 从一个停顿点移动到另一个停顿点也有讲究，而且对于左右手还不一样。有 $m$ 个移动条件，每个移动条件形如：左手在 $a$ 号停顿点时能移动到 $b$ 号停顿点且在 $b$ 号停顿点时也能移动到 $a$ 号停顿点，或右手在 $a$ 号停顿点时能移动到 $b$ 号停顿点且在 $b$ 号停顿点时也能移动到 $a$ 号停顿点。对于某一秒末，蓑笠翁的手没那么快，所以每只手至多只能进行移动一次。上面未提到的移动方式均为非法。 蓑笠翁希望能发动连击。即先发动第 $i$ 种绝招，经过 $t$ 秒的移动后，又发动了第 $j$ 种绝招，且 $i \neq j$。 给出 $p_1, \ldots , p_n$，$v_1, \ldots v_k$，$u_1, \ldots , u_k$，$d_{min}$，$d_{max}$，和 $m$ 个移动条件，现在蓑笠翁想知道，发动第 $i$ 种绝招之后，最少经过多少秒的移动后能发动某个编号不为 $i$ 的绝招，即发动连击的最短耗时。请对于每个 $1 \leq i \leq k$ 输出答案。

 第一行两个正整数 $n,m$。 第二行两个非负整数 $d_{min}, d_{max}$。保证 $d_{min} \leq d_{max}$。 接下来 $n$ 行，这 $n$ 行中的第 $i$ 行每行两个正整数 $x, y$ 表示 $i$ 号停顿点的坐标。 接下来的一行一个正整数 $k$ 。 接下来 $k$ 行，这 $k$ 行中的第 $i$ 行每行两个正整数 $v, u$ 表示 $i$ 号绝招。左手处于 $v$ 号可停顿点，右手处于 $u$ 号可停顿点时能发动该绝招。保证 $1 \leq v, u \leq n$，不会有两个绝招完全相同，保证 $v, u$ 的曼哈顿距离不小于 $d_{min}$ 不大于 $d_{max}$。 接下来 $m$ 行，每行三个正整数 $a, b, type$，若 $type = 0$ 则表示左手在 $a$ 号停顿点时能移动到 $b$ 号停顿点且在 $b$ 号停顿点时也能移动到 $a$ 号停顿点，若 $type = 1$ 则表示右手在 $a$ 号停顿点时能移动到 $b$ 号停顿点且在 $b$ 号停顿点时也能移动到 $a$ 号停顿点。保证 $1 \leq a, b \leq n$，$type \in \{0, 1\}$。

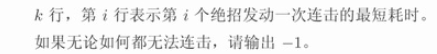
 $k$ 行，第 $i$ 行表示第 $i$ 个绝招发动一次连击的最短耗时。 如果无论如何都无法连击，请输出 $-1$。

5 5
1 6
3 2
9 2
7 3
7 8
4 9
3
5 4
1 3
1 2
1 2 0
2 5 0
1 5 1
1 3 1
3 4 1

2
2
-1

6 14
2 7
3 10
8 9
3 4
6 5
3 10
6 7
4
6 2
1 2
5 2
3 6
5 2 0
4 5 1
2 3 1
5 4 0
1 2 1
1 4 0
6 4 1
5 4 1
4 6 0
1 5 0
4 1 0
6 4 0
5 5 0
1 2 0

2
1
1
-1

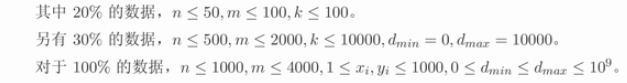
**【样例解释】**  **对于样例一的解释**　对于绝招 $1$，可以先同时将左手移动到 $2$ 号可停顿点，右手移动到 $3$ 号可停顿点，这样耗时 $1 \textrm{ s}$，再将左手移动到 $1$ 号可停顿点，右手不动，这样可以发动绝招 $2$，共用时 $2 \textrm{ s}$。对于绝招 $2$ 可以把刚才的过程反过来，发动绝招 $1$。对于绝招 $3$，无论如何右手都无法移动，不能发动任何绝招，故输出 $-1$。 **对于样例二的解释**　不解释。 **【数据范围】**  其中 $20 \%$ 的数据，$n \leq 50$，$m \leq 100$，$k \leq 100$。 另有 $30 \%$ 的数据，$n \leq 500$，$m \leq 2000$，$k \leq 10000$，$d_{min} = 0$，$d_{max} = 10000$。 对于 $100 \%$ 的数据，$n \leq 1000$，$m \leq 4000$，$1 \leq x_i, y_i \leq 1000$，$0 \leq d_{min} \leq d_{max} \leq {10}^9$。