P5303 [GXOI/GZOI2019] 逼死强迫症
题目描述
ITX351 要铺一条 $2 \times N$ 的路,为此他购买了 $N$ 块 $2 \times 1$ 的方砖。可是其中一块砖在运送的过程中从中间裂开了,变成了两块 $1 \times 1$ 的砖块!
ITX351 由此产生了一个邪恶的想法:他想要在这条路上故意把两块 $1 \times 1$ 的砖块分开铺,**不让两块砖有相邻的边**,其他砖块可以随意铺,直到整条路铺满。这样一定可以逼死自身强迫症 sea5!
也许下面的剧情你已经猜到了——他为此兴奋不已,以至于无法敲键盘。于是,他请你帮忙计算一下,有多少种方案可以让自己的阴谋得逞。
输入格式
每个测试点包含多组数据,输入文件的第一行是一个正整数 $T$,表示数据的组数。注意各组数据之间是独立无关的。
接下来 $T$ 行,每行包含一个正整数 $N$,代表一组数据中路的长度。
输出格式
输出应包含 $T$ 行,对于每组数据,输出一个正整数,表示满足条件的方案数。
由于答案可能非常的大,你只需要输出答案对 $1000000007 (10^9 + 7)$ 取模后的结果。
说明/提示
样例中 $ N=4 $ 解释见下图:
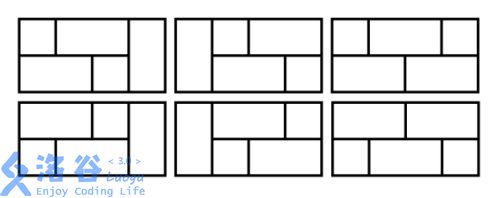
### 数据范围
|测试点编号|$N$ 的规模|$T$ 的规模|
|:-:|:-:|:-:|
|$1$|$N \le 10$|$T \le 10$|
|$2$|$N \le 10$|$T \le 10$|
|$3$|$N \le 10^5$|$T \le 50$|
|$4$|$N \le 10^5$|$T \le 50$|
|$5$|$N \le 10^5$|$T \le 50$|
|$6$|$N \le 2 \times 10^9$|$T \le 50$|
|$7$|$N \le 2 \times 10^9$|$T \le 50$|
|$8$|$N \le 2 \times 10^9$|$T \le 50$|
|$9$|$N \le 2 \times 10^9$|$T \le 500$|
|$10$|$N \le 2 \times 10^9$|$T \le 500$|