【XR-1】逛森林
题目背景
NaCly_Fish 和 PinkRabbit 是好朋友。
有一天她去森林里游玩,回去跟 PinkRabbit 说:“我发现好多棵会动的树耶!”
PinkRabbit 动了动一只兔耳朵:“这有什么好稀奇的,我用一只兔耳朵就能维护每棵树的形态。”
NaCly_Fish 不服:“不止这样,我还看到有一些传送门,能从一条树枝跳到另一条树枝上呢!”
PinkRabbit 动了动另一只兔耳朵:“这有什么好稀奇的,我用两只兔耳朵就能统计每个传送门的信息。”

于是 NaCly_Fish 很郁闷,她向你求助,请帮帮她吧。
什么?你不愿意帮?
那她就不给你这题的分了。
题目描述
给你 $n$ 个节点的森林,初始没有边。
有 $m$ 个操作,分为两种:
$1\ u_1\ v_1\ u_2\ v_2\ w$:表示构建一个单向传送门,从 $u_1 \rightarrow v_1$ 简单路径上的所有节点,可以花费 $w$ 的代价,到达 $u_2 \rightarrow v_2$ 简单路径上的所有节点。若 $u_1$ 到 $v_1$ 或 $u_2$ 到 $v_2$ 不连通(由 $2$ 操作产生的边不连通),则忽略此次操作。
$2\ u\ v\ w$:表示将 $u$ 和 $v$ 节点间连一条花费为 $w$ 的无向边,若 $u$ 和 $v$ 之间已连通(由 $2$ 操作产生的边连通)则忽略此次操作。
经过这 $m$ 次操作后,请你求出从 $s$ 节点出发,到每个节点的最小花费。
输入输出格式
输入格式
第一行三个正整数 $n, m, s$,分别表示树的节点数、操作数、和起始节点。
接下来 $m$ 行,每行若干个正整数,表示一次操作。
输出格式
输出一行 $n$ 个整数,第 $i$ 个整数表示从 $s$ 节点出发,到 $i$ 节点的最小花费。特别地,若不能到达$i$节点,则输出 `-1`。
输入输出样例
输入样例 #1
9 11 5
2 2 1 2
2 3 1 5
2 4 2 10
2 5 3 9
2 6 5 3
2 7 6 6
2 8 7 2
2 9 4 2
1 1 1 4 9 2
1 8 5 1 6 1
1 3 6 9 6 1输出样例 #1
1 1 1 1 0 1 7 9 1说明
【样例说明】
这是样例中给出的树(严格来讲,这棵树也是一条链):
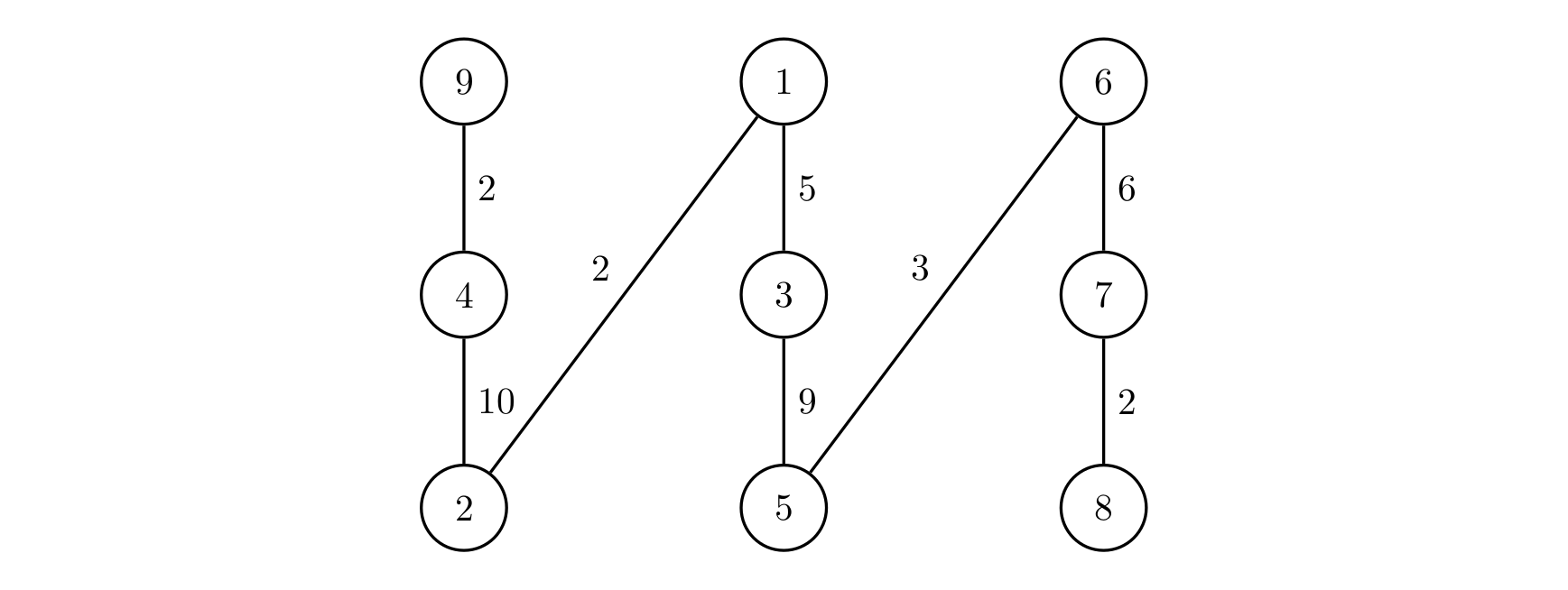
有三个传送门,其中两个是这样的:
- 从 $1$ 号点可以花费 $2$ 的代价到达 $4 \rightarrow 9$ 简单路径上的所有节点(即 $4, 9$ 号点)。
- 从 $8 \rightarrow 5$ 简单路径上的所有节点(即 $8, 7, 6, 5$ 号点)可以花费 $1$ 的代价到达 $1 \rightarrow 6$ 简单路径上的所有节点(即 $1, 3, 5, 6$ 号点)。
容易看出从 $5$ 号节点出发,到达其它节点的最小花费分别为:$1, 1, 1, 1, 0, 1, 7, 9, 1$。
【数据规模与约定】
对于第 $1, 2$ 个测试点,$1 \le n \le 100$,$1 \le m \le 300$。
对于第 $3, 4$ 个测试点,$1 \le n \le 1000$,$1 \le m \le 3000$。
对于 $100\%$ 的数据,$1\le n \le 50000$,$1\le m \le 10^6$,$1\le u,v \le n$,$1\le w \le 100$。
对于第 $1$ ~ $10$ 个测试点,每个 $5$ 分。
对于第 $11, 12$ 个测试点,每个 $25$ 分。