P5465 [PKUSC2018] 星际穿越

有 $n$ 个星球，它们的编号是 1 到 $n$，它们坐落在同一个星系内，这个星系可以抽象为一条数轴，每个星球都是数轴上的一个点，特别地，编号为 $i$ 的星球的坐标是 $i$。 一开始，由于科技上的原因，这 $n$ 个星球的居民之间无法进行交流，因此他们也不知道彼此的存在。现在，这些星球独立发展出了星际穿越与星际交流的工具。对于第 $i$ 个星球，他通过发射强力信号，成功地与编号在 $[l_i,i-1]$ 的所有星球取得了联系(编号为 1 的星球没有发出任何信号)，取得联系的两个星球会建立 **双向** 的传送门，对于建立了传送门的两个星球 $u,v$，$u$ 上的居民可以花费 1 单位时间传送到 $v$，$v$ 上的居民也可以花费 1 单位时间传送到 $u$ ，我们用 $dist(x,y)$ 表示从编号为 $x$ 的星球出发，通过一系列星球间的传送门，传送到编号为 $y$ 的星球最少需要花费的时间。 现在有 $q$ 个星际商人，第 $i$ 个商人初始所在的位置是 $x_i$, 他的目的地是 $[l_i,r_i]$ 中的其中一个星球，保证 $l_i

无

无

样例对应的无向图如下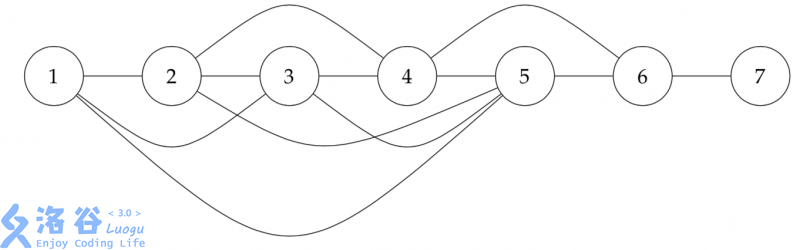： 对于 $20\%$ 的数据，满足 $n \leq 100$。 对于另 $25\%$ 的数据，满足 $n\leq 2000$ 对于另 $25\%$ 的数据，满足 $n\leq 5000$ 对于 $100\%$ 的数据，满足 $n,q\leq 3\times 10^5$