「SWTR-2」Triangles
题目背景
小 $\mathrm{A}$ 在学数学。
题目描述
他遇到了两个谜题:
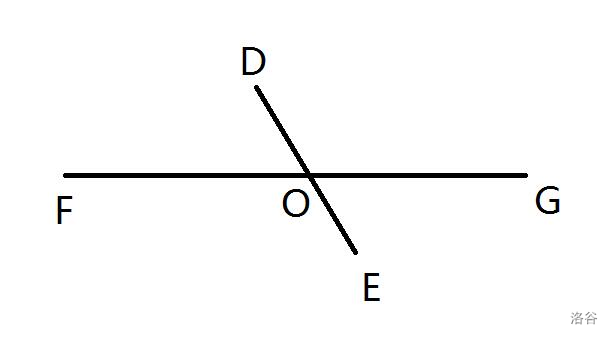
- 在一个平面内,**线段** $DE$ 与**直线** $FG$ 相交于点 $O$,已知 $\angle DOF=x^{\circ}$,请你在**直线** $FG$ 上找一点 $P$,使得 $\triangle DOP$ 为**等腰**三角形,求 $\angle D$ 的度数。(如果答案不是整数,则保留 $1$ 位小数)
- 已知一个**直角三角形**的两条边分别为 $m,n$,求第三条边的长度(保留 $5$ 位小数)。
写一个程序求出问题的答案。
输入输出格式
输入格式
一行三个**正整数**,分别为 $x,m,n$。
输出格式
输出两行,第一行为第一问的答案,第二行为第二问的答案。
如果有多解,请用**空格**隔开,且**从小到大**输出。
输入输出样例
输入样例 #1
60 1 1输出样例 #1
30 60
1.41421说明
---
### 样例说明
问题 $1$:
- 当点 $P$ 在点 $O$ 左边时,形成的 $\triangle DOP$ 为等边三角形,$\angle D=60^{\circ}$。
- 当点 $P$ 在点 $O$ 右边时,形成的 $\triangle DOP$ 中,$\angle DOP=180^{\circ}-60^{\circ}=120^{\circ}$,为顶角,$\angle D=(180^{\circ}-120^{\circ})/2=30^{\circ}$。
问题 $2$:
第三条边为斜边,长度为 $\sqrt{1^2+1^2}=\sqrt{2}=1.41421\dots$。
---
### 数据范围与约定
$x<90,m\leq n\leq 10^9$。
---
### 出题组提示:
**方法千万条,审题第一条,多解不考虑,爆零两行泪。**