轴对称

小 W 学习了轴对称变换。

小 W 觉得轴对称变换实在太好玩了，于是在平面上随机点了 $n$ 个点 $A_1,A_2,\cdots,A_n$，然后进行了一系列轴对称变换，得到了 $B_1,B_2,\cdots,B_n$ 这 $n$ 个点，其中 $A_1$ 得到 $B_1$，以此类推。 可是他突然忘记自己是怎么变换到的了，所以他请你帮他找到一组步数尽量少的合法的变换。

第一行一个整数 $n$，表示点的个数。 接下来 $n$ 行，第 $i+1$ 行两个实数 $x,y$，表示 $A_i$ 的横、纵坐标。 接下来 $n$ 行，第 $i+n+1$ 行两个实数 $x,y$，表示 $B_i$ 的横、纵坐标。

第一行一个整数 $k$ ，表示最少的步数。 接下来 $k$ 行，第 $i+1$ 行三个实数 $A,B,C$，表示第 $i$ 次轴对称变换的轴为直线 $Ax+By+C=0$。

2
1.000000 1.000000
2.000000 2.000000
4.000000 4.000000
3.000000 3.000000

1
1.000000 1.000000 -5.000000

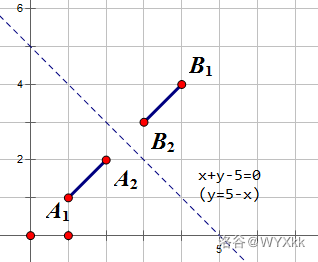
## 样例解释  ## 提示 对于直线 $Ax+By+C=0$，如果 $B$ 非零，那么它就是一次函数 $y=-\dfrac ABx-\dfrac CB$ 的图像；否则，它表示一条垂直于 $x$ 轴的直线 $x=-\dfrac CA$。 本题带有 $\text{SPJ}$。**因为某种原因，本题不提供** $\text{SPJ}$ **给选手。** 对于每个测试点，如果你的 $k$ 正确，则获得 $30\%$ 的分数； 接下来，我们将对 $A_1,A_2,\cdots,A_n$ 分别进行你给的 $k$ 次轴对称变换，记 $A_i$ 得到的点为 $C_i$。如果对于所有的 $i$，$B_i$ 与 $C_i$ 的 $x,y$ 坐标之差的绝对值都不超过 $10^{-2}$，则你获得 $100\%$ 的分数。 如果你只想输出 $k$，也请在后面随意输出一些值，防止 $\text{UKE}$。 ## 数据范围 | 测试点编号 | $n=$ | 构造数据时翻折的次数 | | ---------- | ---- | -------------------- | | 1,2 | $1$ | $\le1$ | | 3,4 | $2$ | $\le10$ | | 5,6 | $5$ | $\le10^3$ | | 7,8,9,10 | $10$ | $\le10^5$ | 对于所有数据，$1\le n\le10$，$|x|,|y|\le 10^5$。 所有数据点已经经过 $\text{SPJ}$ 验证无误。 请保证你的输出中的所有 $A,B,C$ 满足 $|A|,|B|,|C|\le 10^5$。