[Cnoi2020] 光图
题目背景
> 简洁中蕴含着伟大。
Cirno 不经意地把一个内部完全反射的圆分成了 $12$ 等分，等分点分别记作 $A_0$, $A_1$, $A_2$, $\cdots$ , $A_{11}$。
随后，她不经意地将一束光从一点发出，朝向另一点，重复，反射，迭代，便得到了一幅美妙的光图。
这一切都发生在不经意之间。
她不经意地发现了这一幕，并且不经意地记下了这个不经意的结论，又在某一刻不经意地回忆起。
幻想乡的每一天一切都是这么不以为意，多好的一天啊！
题目描述
Rumia 有一个单位圆，被分成 $n$ 等分，等分点分别记作 $A_0$, $A_1$, $A_2$, $\cdots$ , $A_{n-1}$。
现在她从 $A_0$ 向 $A_p$ 发射一束光，经过 $k$ 次反射，到达了 $A_t$。
Rumia 想知道 $t$ 的值，由于 Cirno 并不想帮她，所以 Rumia 转而求助于你。
输入输出格式
输入格式
一行，三个整数，$n,p,k$。
输出格式
一行，一个整数 $t$。
输入输出样例
输入样例 #1
12 5 2输出样例 #1
10输入样例 #2
1000 342 3472844输出样例 #2
648说明
### Sample1 解释
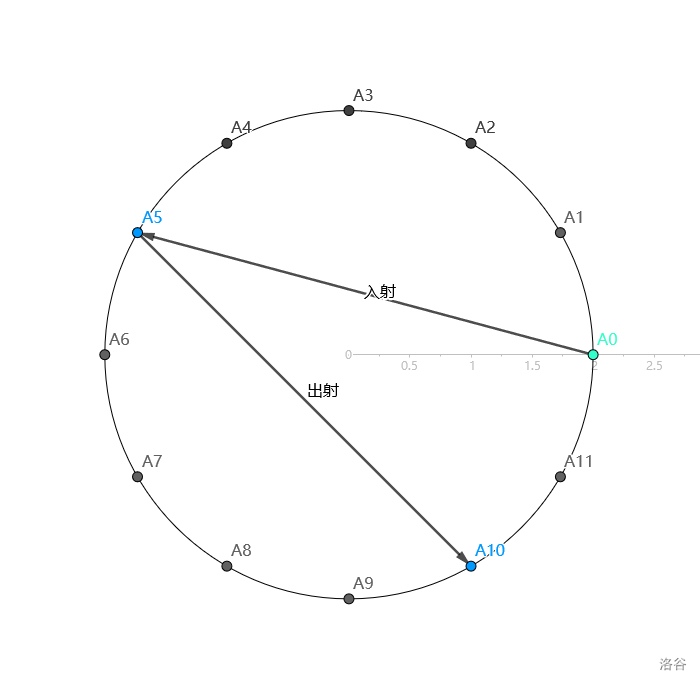
### 后置物理知识
- **连续曲线反射规律** : 入射光线与出射光线关于入射点在曲线上切线夹角相等。
### 数据范围约定
**「本题采用捆绑测试」**
- Subtask1( $80\%$ ) : $n, k \le 10^6$
- Subtask2( $20\%$ ) : $n, k \le 10^9$
对于 $100\%$ 的数据 : $0 < p < n \le 10^9$, $0 < k \le 10^9$。
### 后记
- Cirno 得到的光图就是传说中的**十二芒星图**。