[Cnoi2020] 向量

> 向量(vector)，指具有大小(Magnitude)和方向(Direction) 的量。 > 与向量对应的量叫做数量(Scalar)，数量只有大小，没有方向。 对于 Cirno 来说，整天环绕氷屋的旋转 Sangetsusei 们是向量而不是数量。 - Sunny Milk 以 $r_1$ 为半径做匀速圆周运动。 - Luna Child 以 $r_2$ 为半径做匀加速圆周运动。 - Star Sapphire 以 $r_3$ 为半径做变加速圆周运动。 为了尽可能的减小三月精们的影响，一些重要的参数必需被计算。

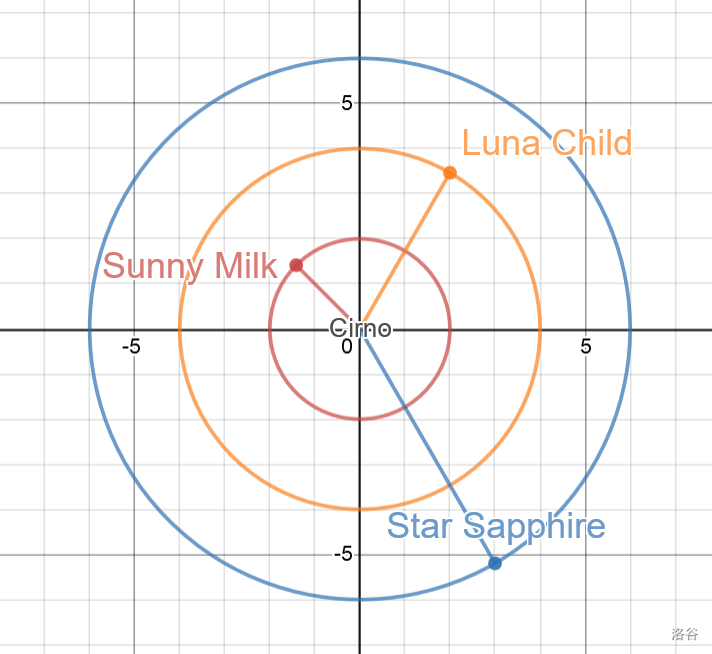
以氷屋为原点，三月精的位置分别记作向量 $\vec{a}$, $\vec{b}$, $\vec{c}$。  由定义可知，$|\vec{a}|=r_1$, $|\vec{b}|=r_2$, $|\vec{c}|=r_3$。 现在 Cirno 分配给你的任务是计算其 **破坏极限指数** $\sigma$。 $$\sigma=\min\{\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{c}+\vec{c}\cdot\vec{a}\}$$ 其中「$\cdot$」表示 **向量内积**。

一行，三个整数 $r_1$, $r_2$, $r_3$，保证 $r_1 \le r_2 \le r_3$。

一行，一个 **实数** $\sigma$。（**小数点后保留一位数字**）

3 4 5

-25.0

159 473 824 

-445561.0

### Sample1 解释 $\cos\langle\vec{a},\vec{b}\rangle=0,\cos\langle\vec{b},\vec{c}\rangle=-\frac{4}{5},\cos\langle\vec{c},\vec{a}\rangle=-\frac{3}{5}$ 时答案最小。 ### 后置数学知识 - **向量内积定义** : $\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\times \cos\langle\vec{a},\vec{b}\rangle$ - **向量内积坐标表示** : $(x_1,y_1)\cdot(x_2,y_2)=x_1x_2+y_1y_2$ ### 数据范围约定 **「本题采用捆绑测试」** - Subtask1( $20\%$ ) : $r_1=r_2=r_3$ - Subtask2( $40\%$ ) : $r_1,r_2,r_3 \le 10$ - Subtask3( $40\%$ ) : $r_1,r_2,r_3 \le 10^9$ 对于 $100\%$ 的数据 $0 < r_1 \le r_2 \le r_3 \le 10^9$