P6344 [CCO 2017] Vera 与现代艺术
题目描述
在受到大画家毕加索的启发后,Vera 决定创造她的杰作。她有一张可以被简化成无限大的二维平面的画布。Vera 喜欢 $2$ 的整数次幂 $(1,2,4,8,16,...)$,并且将以 $2$ 的整数幂为步长给一些点染色。
Vera 将会染 $n$ 次,第 $i$ 次染色可以用三个整数 $x_i,y_i,v_i$ 描述。令 $a_i$ 为最大的不大于 $x_i$ 的 $2$ 的整数次幂,$b_i$ 为最大的不大于 $y_i$ 的 $2$ 的整数次幂,Vera 会用第 $v_i$ 种颜色在所有坐标满足 $(x_i+a_ip,y_i+b_iq)$ 的点上染色( $p,q$ 为非负整数)。一个点可以被不同的颜色分别染多次,也可以被同种颜色重复染多次,一个点的颜色为所有染过这个点的颜色之和。
接下来 Vera 将提出 $Q$ 个问题。对于第 $j$ 个问题,她希望知道坐标为 $(r_j,c_j)$ 的点是什么颜色。如果一个点没有被染过色,这个点的颜色就为 $0$。
因为你被迫做 Vera 的助手,你不得不回答 Vera 的问题。
输入格式
无
输出格式
无
说明/提示
#### 样例解释
令颜色 $1,2,3,4,5$ 分别为红色、蓝色、绿色、橙色和紫色。
令 $p,q$ 为非负整数,则:
- 坐标为 $(1+p,2+2q)$ 的点被染成了红色;
- 坐标为 $(3+2p,4+4q)$ 的点被染成了蓝色;
- 坐标为 $(4+4p,5+4q)$ 的点被染成了绿色;
- 坐标为 $(6+4p,3+2q)$ 的点被染成了橙色;
- 坐标为 $(7+4p,1+q)$ 的点被染成了紫色;
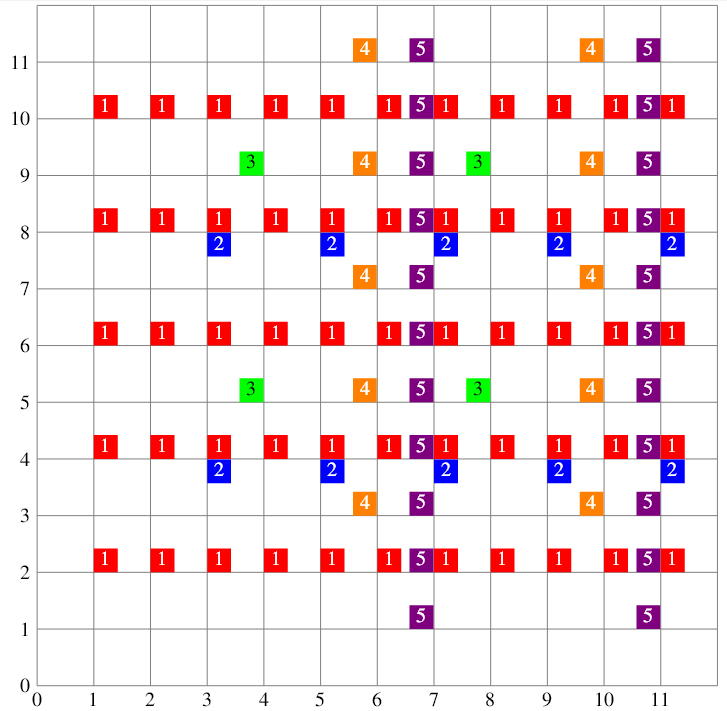
从 $(0,0)$ 到 $(11,11)$ 的坐标纸如图所示:
我们可以发现:
- $(2,6)$ 被染成了红色,所以它的颜色为 $1$;
- $(7,8)$ 被染成了红色、蓝色和紫色,所以它的颜色为 $1+2+5=8$;
- $(5,9)$ 没有被染色,所以它的颜色为 $0$;
- $(11,2)$ 被染成了红色和紫色,所以它的颜色为 $1+5=6$;
- $(10,7)$ 被染成了橙色,所以它的颜色为 $4$;
- $(4,5)$ 被染成了绿色,所以它的颜色为 $3$。
#### 数据范围及约定
- 对于 $20\%$ 的数据,$1 \le n,Q \le 2 \times 10^3$ ;
- 对于另外 $20\%$ 的数据,$y_i = 1(1 \le i \le n)$;
- 对于另外 $20\%$ 的数据,$1 \le n,Q \le 10^5$ 且 $1 \le r_j,c_j \le 10^9(1 \le j \le Q)$。
- 对于 $100\%$ 的数据,$1 \le n,Q \le 2 \times 10^5$,$1 \le i \le n$,$1 \le v_i \le 10^4$,$1 \le x_i,y_i,r_j,c_j \le 10^{18}$,$1 \le j \le Q$。
由于评测机原因,该题只保留最后 $10$ 个数据。
来源:[CCO 2017](https://cemc.math.uwaterloo.ca/contests/computing/2017/index.html) Day1「[Vera and Modern Art](https://cemc.math.uwaterloo.ca/contests/computing/2017/stage%202/day1.pdf)」。
说明:翻译来自 [LOJ](https://loj.ac/problem/2752)。