重拳出击

小 Z 和 $m$ 个 Youyou 在一棵树上相遇了！ 这棵树上，每条边的长度都是 $1$。 初始时，小 Z 在 $x$ 号节点上，并且有一把射程为 $k$ 的枪。 因为小 Z 技术精湛，所以 Youyou 一打就死，而小 Z 永远不会死掉。 小 Z 和 Youyou 都按回合行动，在每一回合中，按照下面的顺序行动： 1. 回合计数器 $+1$（初始为 $0$）。 2. 小 Z 可以用枪射死与小 Z 树上距离小于等于 $k$ 的所有 Youyou。 3. 如果所有 Youyou 都被消灭了，游戏结束，这时回合计数器的值就是小 Z 用的回合数。 4. 小 Z 可以选择沿着一条边，移动到任意相邻节点，也可以选择不动。 5. 所有 Youyou 都会沿着他和小 Z 的简单路径向小 Z 移动一条边的距离。如果此时他们在同一个节点，则不动。 小 Z 需要求出消灭所有敌人需要的最小回合数。

第一行一个正整数 $n$。 接下来 $n-1$ 行每行两个正整数，表示这棵树上的一条边。 接下来一行一个正整数 $m$。 接下来一行 $m$ 个正整数，第 $i$ 个数表示第 $i$ 个 Youyou 的初始所在节点。 最后一行两个整数，$k$ 和小 Z 自己的初始所在节点号 $x$。

一行一个正整数，最小回合数。

5
1 2
2 3
3 4
4 5
5
1 2 3 4 5
0 3

3

5
1 2
1 3
2 4
2 5
4
1 1 2 2
1 5

2

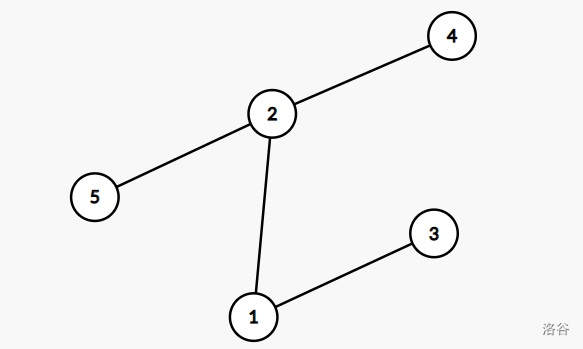
**样例 2 解释**  小 Z 可以在第一回合射死后两个 Youyou，然后从节点 $5$ 移动到节点 $2$。剩余的两个 Youyou 也会移动到节点 $2$。第二回合小 Z 可以消灭所有 Youyou。可以证明这就是最优方案。 **数据规模与约定** * Subtask 1（10 分）：$1 \le n,m \le 20$； * Subtask 2（15 分）：$1 \le n,m \le 2\times 10^3$； * Subtask 3（30 分）：$1 \le n,m \le 4\times 10^4$； * Subtask 4（45 分）：$1 \le n,m \le 4\times 10^5$。 对于全部的数据，$1 \le n,m \le 4\times 10^5$，$0 \le k \le 10^6$。