[YsOI2020] 换寝室

马上要开学了，Ysuperman 正在为给孩子们分配寝室忙得不可开交......

幼儿园里面有 $n$ 个房间，这些房间由 $n-1$ 条双向道路连接着，第 $i$ 条道路连接着房间 $u_i$ 和 $v_i$ ，每条道路 Ysuperman 都可以选择开启或者是关闭，每个房间**在所有道路开启的前提下**都可以到达其他任意一个房间。 每个房间有一个差异值，其中，第 $i$ 个房间的差异值为 $h_i$ 。 在选择完关闭哪些道路后，整个寝室会被分成许多连通块，一个联通块内的小朋友的不满意值定义为连通块内差异值的**最大值减去最小值**，小朋友们的总不满意值定义为**所有联通块不满意值的最大值**。 寝室里有 $m$ 个寝室老师，每个老师晚上都要查寝，第 $i$ 个老师会从第 $x_i$ 个房间走到第 $y_i$ 个房间，如果老师在查寝时经过了某条被关闭的道路，TA就会很生气，一个老师的不满意值定义为**从 $x_i$ 走到 $y_i$ 经过的被关闭的道路数量**，老师的总不满意值定义为**所有老师的不满意值之和**。 Ysuperman 能承受的老师的总不满意值最大为 $k$ ，现在TA想知道小朋友们的总不满意值最小可以达到多少。

输入共 $n+m+1$ 行。 第一行三个整数 $n,m,k$，表示房间个数，寝室老师个数和Ysuperman 能承受的老师的总不满意值。 接下来一行，共 $n$ 个整数，第 $i$ 个整数是 $h_i$，表示第 $i$ 个房间的差异值。 接下来 $n-1$ 行，每行两个整数，第 $i+2$ 行是 $u_i$ 和 $v_i$，表示寝室 $u_i,v_i$ 之间有直接道路。 接下来 $m$ 行，每行两个整数，第 $i+n+1$ 行是 $x_i$ 和 $y_i$，表示第 $i$ 个老师的查寝路线。

一行一个整数，即答案。

5 2 0
1 3 1 4 0
1 2
1 3
1 4
1 5
2 3
1 4

3

5 2 1
1 3 1 4 0
1 2
1 3
1 4
1 5
2 3
1 4

2

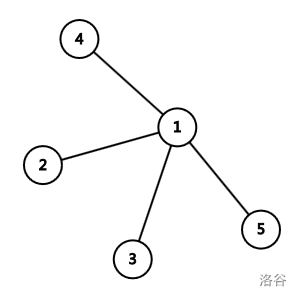
### 样例说明 #### 样例说明 $1$  Ysuperman选择关闭连接着 $1$ 和 $5$ 的道路，老师的总不满意值为 $0$，寝室被分为 $2$ 个连通块，小朋友们的总不满意值为 $3$。 #### 样例说明 $2$ 图同样例一。 Ysuperman选择关闭连接着 $1$ 和 $5$ 的道路以及连接着 $1$ 和 $4$ 的道路，老师的总不满意值为 $1$，寝室被分为 $3$ 个连通块，小朋友们的总不满意值为 $2$。 ------ ### 数据范围 **本题采用捆绑测试。** | Subtask | $n$ | $m$ | $k$ | 特殊性质 | 分数 | |:-:|:-:|:-:|:-:|:-:|:-:| | 1 | $\le 20$ | $\le 10$ | $\le 80$ | 无 | 8 | | 2 | $\le 150$ | $\le 10^3$ | $\le 8 \times 10^4$ | 无 | 13 | | 3 | $\le 800$ | $\le 10^5$ | $\le 8 \times 10^7$ | 树为一条链 | 13 | | 4 | $\le 800$ | $\le 10^5$ | $\le 8 \times 10^7$ | 树为一朵盛开的菊花 | 13 | | 5 | $\le 800$ | $\le 10^5$ | $= 0$ | 无 | 13 | | 6 | $\le 800$ | $\le 10^5$ | $\le 8 \times 10^7$ | 无 | 40 | 【一条链】定义为：所有点的度数 $\le2$。 【一朵盛开的菊花】定义为：存在一个点的度数为 $n-1$。 对于 $100\%$ 的数据，满足 $1\le h_i\le 10^9，0\le k \le 8\cdot 10^7,u_i\ne v_i$ 。