「EZEC-2」机器

tlx 喜欢科幻小说。 >小宇宙中只剩下漂流瓶和生态球。漂流瓶隐没于黑暗里,在一千米见方的宇宙中,只有生态球里的小太阳发出一点光芒。在这个小小的生命世界中,几只清澈的水球在零重力环境中静静地飘浮着,有一条小鱼从一只水球中蹦出,跃入另一只水球,轻盈地穿游于绿藻之间。在一小块陆地上的草丛中,有一滴露珠从一片草叶上脱离,旋转着飘起,向太空中折射出一缕晶莹的阳光。 >$\qquad \qquad \qquad \qquad \qquad \qquad \qquad\qquad\qquad\qquad\qquad\qquad\qquad --$《三体》 在另一个宇宙，将是另一番奇景吧。 在那里，重力似乎变得微不足道了，引力机器成了司空见惯的东西。 引力机器装置内并没有重力，即若有物体在机器上运动，运动过程中只受机器给予的引力，这个力有一定几率使物体向施力物体快速移动，达到一定动力时就可以实现瞬移。

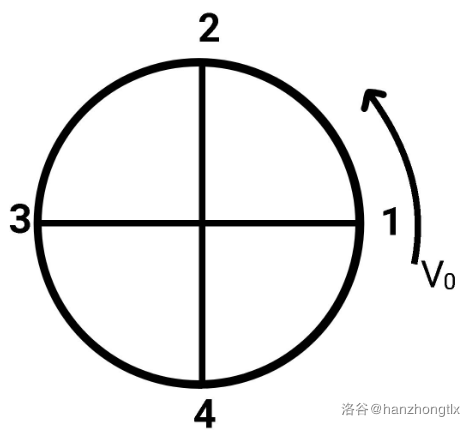
一个引力机器由一个光滑圆轨道和 $2n$ 个小孔组成（小孔按**逆时针**从 $1$ 到 $2n$ 编号，每两个相邻的小孔所夹的**劣弧**度数为 $\dfrac{\pi}{n}$ ），每个小孔与和其夹角为 $\pi$ 的另一个小孔有通道相连，比如当 $n=2$ 时，$1$ 号孔和 $3$ 号孔相连。 当 $n=2$ 时，这个装置的构造大概是这样的：  现在我们在 $1$ 号孔处放一个小球，使它一直**沿逆时针方向做匀速圆周运动**，在不瞬移的情况下，每一秒恰好能从一个小孔运动至下一个小孔。 由于未来实验室构造奇特（内部的引力提供装置太神了！），每经过一个小孔时，有 $p$ 的概率**立刻瞬移**（即不花费时间）到通道对面的小孔并继续沿逆时针方向做匀速圆周运动，也就是有 $1-p$ 的概率继续沿圆周向下一个小孔运动。 值得注意的是，**每一单位时刻，小球只能瞬移一次**。 简单地说，若某一时刻小球在小孔 $i$，则下一时刻它可能运动到小孔 $i \bmod 2n + 1$ 或 $(i + n) \bmod 2n + 1$，概率分别为 $1-p$ 和 $p$。 现在 tlx 有两个一模一样的引力机器，两个小球同时从 $1$ 号孔开始运动。他会**随机**（所有可能选择的概率相同）选择一个二元组 $(i,j)( 1\leqslant i\leqslant 2n,0\leqslant j\leqslant t,i,j\in \mathbb Z$ ) 分别代表小孔编号和时间，你需要求出时间为 $j$ 时两个引力机器的小孔 $i$ **同时**有小球**停留（运动经过小孔但瞬移到对面了不算停留）** 的概率。 注意：**小球刚开始运动时也可能瞬移到对面的小孔。** 为方便计算，我们规定：所有概率都是在模 $10^9+7$ 意义下的。

输入数据共一行，三个整数 $n,p,t$，分别代表引力装置的小孔数的一半，瞬移的概率对 $10^9+7$ 取模的结果，选择的时间的范围的上界。

共一行，一个整数，代表两个小球同时经过所选位置的概率对 $10^9+7$ 取模的结果。

2 500000004 1

125000001

6 114514 11

756497239

**【数据范围与约定】** **本题采用捆绑测试。** 具体计分方式如下： - Subtask $1$ ($7$ points)：满足 $p\in \{0,1\}$； - Subtask $2$ ($13$ points)：满足 $t\leqslant 20,n\leqslant50$； - Subtask $3$ ($20$ points)：满足 $t\leqslant 10^3,n\leqslant50$； - Subtask $4$ ($10$ points)：满足 $t\leqslant 10^3$； - Subtask $5$ ($10$ points)：满足 $t\leqslant 10^6$； - Subtask $6$ ($15$ points)：满足 $n\leqslant50$； - Subtask $7$ ($25$ points)：无特殊限制。 对于 $100\%$ 的数据，满足 $2\leqslant n\leqslant 500$，$0\leqslant p\leqslant 10^9+6$，$0\leqslant t \leqslant 10^9$。 **注意：不做说明的数据范围即为极限数据范围。** **【样例解释 #1】** $500000004$ 是模 $10^9+7$ 意义下的 $\dfrac{1}{2}$。 下面为了方便，记 $P(i,j)$ 为选择的二元组为 $(i,j)$ 时的概率。 所有概率不为 $0$ 的二元组有： $P(1,0)=\dfrac{1}{4},P(3,0)=\dfrac{1}{4},P(2,1)=\dfrac{1}{4},P(4,1)=\dfrac{1}{4}$。 所有可以选择的二元组有： $(1,0),(1,1),(2,0),(2,1),(3,0),(3,1),(4,0),(4,1)$，共 $8$ 种。 所以总的概率： $$P=\dfrac{1}{8}×\dfrac{1}{4}×4+\dfrac{1}{8}×0×4=\dfrac{1}{8}$$ 在模 $10^9+7$ 意义下为 $125000001$，即为输出的答案。 ------------ **【其他提示】** 1. 如果你不了解分数取模，可以查看[这里](https://www.luogu.com.cn/problem/P2613)。 2. 如果你不明白题目中角度的表示方法，可以查看[弧度制](https://baike.baidu.com/item/弧度制/3315973?fr=aladdin)。