『MdOI R3』Fallen Lord

统治着世界，统治着寂寞。

L 国有 $n$ 个城市，它们之间有 $n-1$ 条道路，形成了一棵树的结构。 国王 L 派遣了一些军队来驻守这些道路，驻守每一条道路的军队战斗力都可以被量化为 $[1,m]$ 中的整数。 每个城市都有一个城主，第 $i$ 个城主有一个忍耐度 $a_i$。如果国王 L 在与第 $i$ 个城市相连的所有道路上驻守的军队战斗力的**中位数**超过了**城主**的忍耐度，那么**城主**就会认为国王不信任他而产生谋反的心理。 国王 L 当然不希望有人造反，但他又想使驻守道路的军队的总战斗力**最大**来保证国防安全。现在他找到了 L 国最强的 OIer —— 您，去来帮助他解决这个问题。 如果无论如何安排军队都会有人想要造反，那么输出 `-1`。 **注：对于任意 $k$ 个数，它们的中位数是将这些数从小到大排序后第 $\left\lfloor\dfrac{k}{2}\right\rfloor+1$ 个数。**

第一行两个正整数，表示 $n,m$。 第二行 $n$ 个整数，第 $i$ 个数表示 $a_i$。 接下来 $n-1$ 行，每行两个数 $u_i,v_i$，表示一条直接连接城市 $u_i$ 与城市 $v_i$ 的道路。 **输入数据保证构成一棵树**。

一行一个整数，表示最大的总战斗力。

7 100
50 25 25 12 12 12 12
1 2
1 3
2 4
2 5
3 6
3 7

148

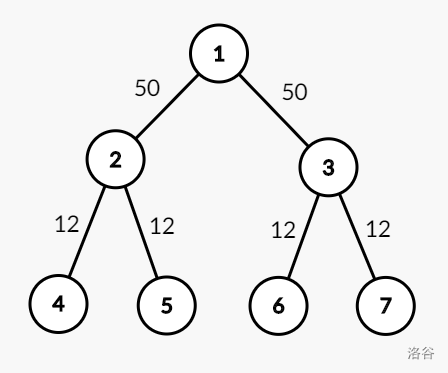
更多样例请[到这里](https://www.luogu.com.cn/paste/0wcdzik5)领取。 对于所有数据，$1\le u_i,v_i \le n\le 5\times 10^5$，$n\ge 2$，$1\le a_i\le m\le 10^9$。 |子任务编号|$n\leq$|$m\leq$|其他性质|分值| |:-:|:-:|:-:|:-:|:-:| |1|$8$|$8$|无|$5$| |2||$1$|无|$1$| |3|||树的形态为一条链|$10$| |4|||存在度数为 $n-1$ 的节点|$12$| |5|$10^5$||每个节点度数 $\le 6$|$17$| |6|$5\times 10^3$||无|$20$| |7|||无|$35$| 其中，留空的表示和 $100\%$ 的数据范围限制相同。 ### 样例解释  如图驻守 $n-1=6$ 条道路的军队战斗力（按照输入中的顺序）依次为 $50,50,12,12,12,12$。