「MCOI-02」Glass 玻璃

小 S 进入了一个服务器，这个服务器有一个游戏叫“树上的玻璃”。

首先给定一棵树，每个点上有 $V_i$ 个玻璃，每条边上有权值 $W_i$。 每次操作小 S 可以选择两个节点 $u,v(u\ne v)$，从节点 $u$ 到节点 $v$ 的唯一路径上，**边和** 为路径上所有边的权值和，即 $\sum W_i$，**点和** 为路径上所有点（包括 $u,v$）的玻璃数和，即 $\sum V_i$。小 S 将可以获得 **边和** 和 **点和** 的乘积的分数，即 $\sum W_i\times\sum V_i$。 任意两次操作不能完全相同，$(u,v)$ 和 $(v,u)$ 被看作是两种操作。 但是有时候这颗树太过庞大，小 S 需要你的帮助。他需要你告诉他，经过 $N(N-1)$ 次操作后，总共能得到多少分。结果可能很大，你只需要输出答案对 $998244353$ 取模的结果。

第一行一个整数 $N$ 表示树的节点数。 第二行 $N$ 个整数，第 $i$ 个数 $V_i$ 表示节点 $i$ 的玻璃数。 接下来 $N-1$ 行，每行三个数 $x,y,z$，表示节点 $x,y$ 之间连有一条权值为 $z$ 的树边。

一个整数，即总共能得到的分对 $998244353$ 取模。

5
1 2 1 2 1
1 5 1
1 2 2
2 3 1
2 4 2

256

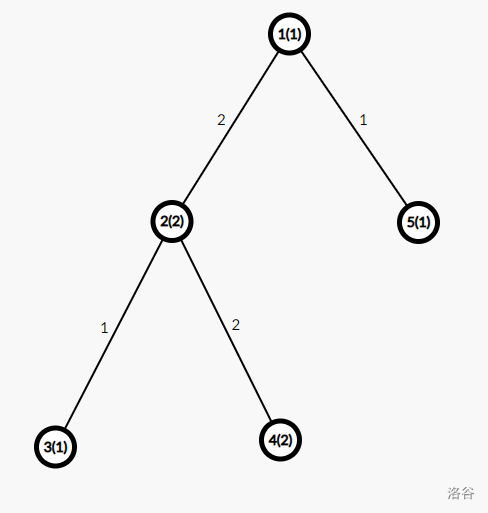
#### 样例说明 对于样例 $1$，树的形态如下：  #### 数据规模与约定 **本题采用捆绑测试。** |子任务编号 | $N$ | $V_i,W_i$ | 特殊性质 | 分值 |时限| | :----------: | :----------: | :----------: | :----------: | :----------: | :----------: | | 1 | $\le200$ | $\lt 2^3$ | | $3$ |$\rm 1s$| | 2 | $\le10^3$ | $\lt2^3$ | | $6$ |$\rm 1s$| | 3 | $\le6\times10^3$ | $\lt2^8$ | | $11$ |$\rm 1s$| | 4 | $\le2\times 10^5$ | $\lt 2^8$ | 存在度数为 $N-1$ 的节点 | $12$ |$\rm 1s$| | 5 | $\le2\times10^5$ | | 树的形态为一条链 | $13$ |$\rm 1s$| | 6 | $\le2\times10^5$ | | | $21$ |$\rm 1s$| | 7 | $\le2\times10^6$ | | | $34$ |$\rm 2s$| 对于 $100\%$ 的数据，$0\le V_i,W_i\lt2^ {16}$，$1 \le N\le2\times10^6$。 #### 说明 Minecraft OI Round 2 D - Maker：Inf_Voltage - Tester：tarjin