移花接木

遥远的圣地生长着一棵不为人知的灵树，或有万山之高。 但有一日，藏匿于根系的腐朽力量爆发，灵树已无法支撑往日屹立冲天的高度。

灵树最初的形态可以看作一棵高度为 ${10}^{{10}^{{10}^{10}}}$ 的满 $a$ 叉树，高度定义为根结点到叶子结点之间的边数。 受腐朽力量影响，灵树只能维持高度**恰好**为 $h$ 的满 $b$ 叉树形态。为了转换至该形态，灵树有两种魔法： - 移花：选择一条边 $u \to v$（$u$ 是 $v$ 的父结点），移除这条边以及以 $v$ 为根的**整棵子树**。 - 接木：选择一条边 $u \to v$（$u$ 是 $v$ 的父结点）和一个结点 $w$（$w$ 不能是 $v$ 子树中或已移除的结点），将这条边原先 $u$ 一端**改接**到 $w$。**该魔法只能在根结点到** $\boldsymbol{u}$ **之间的边数** $\le 10^{10^{10}}$ **时使用。** 灵树累积的魔法力量有限，它不得不用最少次数的魔法完成转换。这是个漫长的过程，即使次数最少也会显得异常大，你只需要求出最少次数对 $10^9 + 7$ 取模的结果。

输入首行给定数据组数 $T$。 接下来 $T$ 行，每行包含三个整数 $a,b,h$，表示一组数据。

对于每组数据输出一行一个整数，表示该数据的答案对 $10^9 + 7$ 取模的结果。

2
1 2 1
3 2 1

2
7

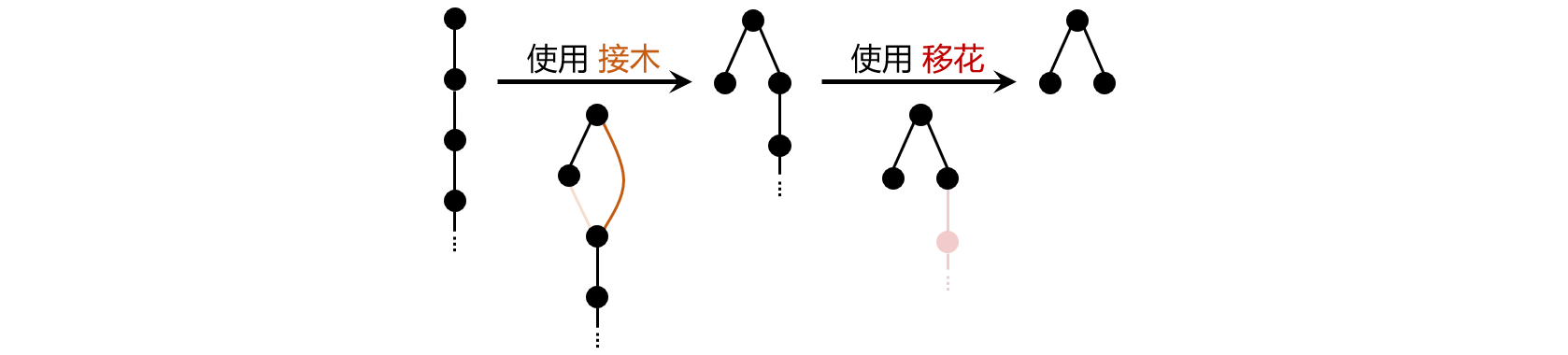
**【样例解释 #1】** 下为 $a=1$，$b=2$，$h=1$ 时的两步转换过程，图中高度极大的冗余子树已用省略号代替。  可以证明，该数据的答案不可能低于 $2$。 ---- **【数据规模与约定】** **本题采用捆绑测试**。你必须通过 Subtask 中所有的测试点才能获得该 Subtask 的分数。 - Subtask #1 (3 points)：$h = 0$。 - Subtask #2 (4 points)：$a = b$。 - Subtask #3 (8 points)：$a = 1$。 - Subtask #4 (8 points)：$b = 1$。 - Subtask #5 (17 points)：$h \le 10$。 - Subtask #6 (15 points)：$h \le 10^6$，各测试点存在 $\overline{a},\overline{b}$，其数据满足 $a=\overline{a}$，$b=\overline{b}$。 - Subtask #7 (15 points)：$h \le 10^6$。 - Subtask #8 (30 points)：无特殊限制。 所有测试点（样例除外）均含有 $10^6$ 组数据，即 $T = 10^6$。请务必采用较快的 IO（输入/输出）方式。 对于所有的数据，保证 $1 \le a,b \le 10^9$，$0 \le h \le 10^9$。