送给好友的礼物

小 M 和小 B 是一对好朋友，她们很喜欢草莓。

给定一棵包含 $n$ 个结点的树 $T$，结点从 $1 \sim n$ 顺序编号。 小 M 和小 B 在时刻 $0$ 都在 $1$ 号结点。从时刻 $1$ 开始的每个时刻初，小 M 和小 B 都可以选择：移动到一个和自己所在结点直接相连的结点，或者停留在当前所在的结点。 树上有 $k$ 个草莓，它们分布在 $k$ 个不同的结点上。小 M 和小 B 想要收集到所有的草莓，任何一个时刻末，如果小 M 或者小 B 在某一个草莓所在的结点上，那么这个草莓就被收集了。 她们不想花费太多的时间，因此你需要回答：至少在第几时刻末，小 M 和小 B 可以收集到所有的草莓，并且都回到结点 $1$。

第一行两个整数 $n, k$（$1 \leq k \leq n \leq 415$），分别表示树的结点个数和草莓的个数。 接下来 $n - 1$ 行，每行两个整数 $u$ 和 $v$，表示树上有一条从 $u$ 到 $v$ 的边。 接下来一行 $k$ 个互不相同的整数 $a_1, a_2, \ldots , a_k$，分别表示这 $k$ 个草莓所在的结点。

一行一个整数，所求答案。

7 4
1 2
2 3
2 4
1 5
5 6
6 7
3 4 5 7

6

1 1
1

0

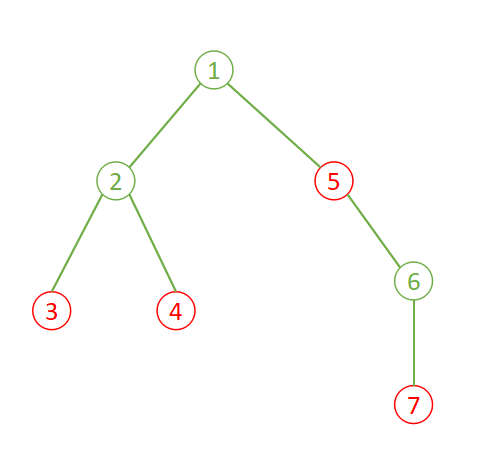
**【样例解释 #1】**  小 M 的路线是：$1 \to 2 \to 3 \to 2 \to 4 \to 2 \to 1$。 小 B 的路线是：$1 \to 5 \to 6 \to 7 \to 6 \to 5 \to 1$。 --- **【数据范围】** **本题采用捆绑测试。** - Subtask 1（$6$ 分）：$n \leq 3$。 - Subtask 2（$1$ 分）：$k = 1$。 - Subtask 3（$11$ 分）：$n \leq 7$。 - Subtask 4（$17$ 分）：$k \leq 20$。 - Subtask 5（$42$ 分）：$n \leq 90$。 - Subtask 6（$23$ 分）：无特殊限制。 对于 $100 \%$ 的数据，$1 \leq k \leq n \leq 415$，$1 \leq u, v \leq n$。