弹珠游戏（2021 CoE-I C）

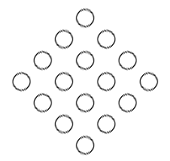
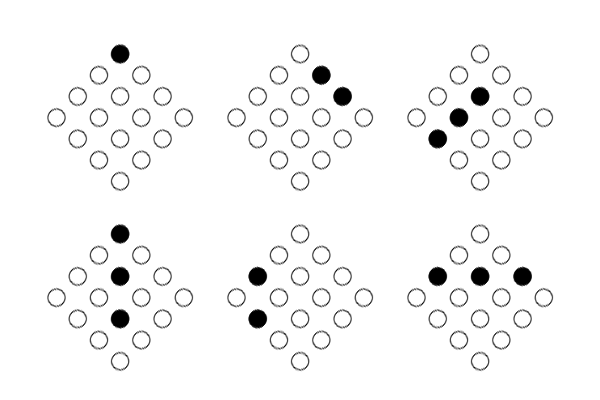
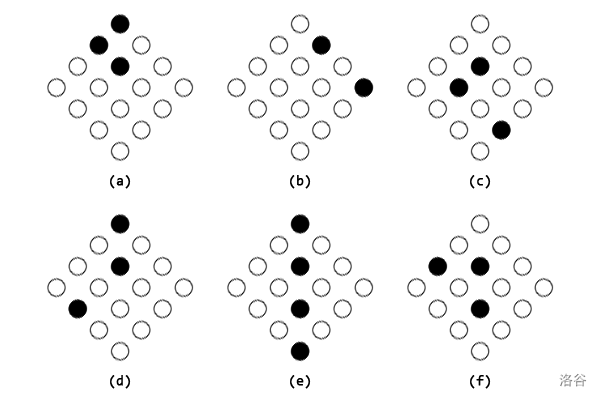
$\operatorname{Alice}$ 对弹珠游戏已经有些厌烦了，她经常在电脑上玩这个游戏。她之所以感到厌烦是因为在这个游戏上她已经是专家级别，她总是能够和电脑打成平手。$\operatorname{Bob}$ 为 $\operatorname{Alice}$ 创造了一款新的电脑游戏。以下是这款两人电脑游戏的规则： （1）游戏在如下图所示的菱形棋盘上进行；  （2）两名玩家轮流放置弹珠，可以在横向、纵向、$45$ 度斜线、$135$ 度斜线方向未放置弹珠的位置**连续放置 $1$ 至 $3$ 颗弹珠**，玩家在可以放置弹珠的情况下，必须至少放置 $1$ 颗弹珠。以下是合法的单次放置操作的示例（黑色圆点表示放置了弹珠，白色圆点表示未放置弹珠，进行该次操作前棋盘为空）：  以下是非法的单次放置操作的示例（黑色圆点表示放置了弹珠，白色圆点表示未放置弹珠，进行该次操作前棋盘为空）：  非法原因的解释：（$a$）三颗弹珠不在同一条斜线（或者垂直线）上；（$b$）两颗弹珠之间相隔一个空位；（$c$）三颗弹珠不在同一条斜线上；（$d$）三颗弹珠不在同一条斜线（或者垂直线）上；（$e$）一次性放置了 $4$ 颗弹珠；（$f$）三颗弹珠不在同一条水平线（或者垂直线、或者斜线）上。 （3）如果某位玩家无法再继续放置弹珠，则该名玩家输掉游戏，另外一名玩家获胜。 $\operatorname{Alice}$ 总是第一个进行游戏，而且经常是和 $\operatorname{Bob}$ 玩这个游戏，$\operatorname{Bob}$ 在进行若干游戏操作后可能会离开，将游戏交由电脑代理，电脑总是按照最优策略放置弹珠。 给定 $\operatorname{Bob}$ 离开后的游戏状态，你的任务是确定 $\operatorname{Alice}$ 是否可能在对阵电脑时获得胜利。

**输入包含多组测试数据**。 输入第一行包含一个整数 $T$，表示测试数据的组数。接着是一个空行。再接下来是 $T$ 组表示棋盘状态的数据，每组数据由七行字符构成，表示 $\operatorname{Bob}$ 离开后的游戏状态，`*` 表示该位置已经放置了弹珠，`.` 表示该位置未放置弹珠。相邻两组测试数据之间有一个空行。

对于每组测试数据，如果 $\operatorname{Alice}$ 能够获胜，输出 `Possible.`，否则输出 `Impossible.`。

6

   *
  * *
 * * *
* * * *
 . * *
  . *
   .

   *
  * *
 * * *
. . . *
 * * *
  * *
   *

   *
  * *
 * * .
* * * *
 * * .
  * *
   *

   *
  * *
 . . *
* * * *
 * * *
  * *
   *

   .
  * *
 * * *
* * * .
 * * *
  * *
   *

   .
  * .
 * * .
* * * .
 * * *
  * *
   *

Possible.
Possible.
Possible.
Possible.
Impossible.
Possible.

#### 样例说明 第一组数据，$\operatorname{Alice}$ 可以选择在棋盘左下角的斜线方向所剩下的 $3$ 个空余位置一次性连续放置 $3$ 颗弹珠，使得后续电脑无法再放置弹珠，因此 $\operatorname{Alice}$ 能够获胜。 第二组数据，$\operatorname{Alice}$ 可以选择沿着第四行剩下的 $3$ 个空余位置一次性连续放置 $3$ 颗弹珠，使得后续电脑无法再放置弹珠，因此 $\operatorname{Alice}$ 能够获胜。 第三组数据，棋盘剩下倒数第二列两个连续的空余位置，$\operatorname{Alice}$ 可以一次放置 $2$ 颗弹珠，使得后续电脑无法放置弹珠，因此 $\operatorname{Alice}$ 会获胜。 第四组数据，类似于第二组测试数据，棋盘剩下第三行两个连续的空余位置，因此 $\operatorname{Alice}$ 会获胜。 第五组数据，棋盘只剩下两个不连续的空余位置，由于 $\operatorname{Alice}$ 一次只能选择一个空余位置放置 $1$ 颗弹珠，因此不管 $\operatorname{Alice}$ 如何操作，电脑总能一次性将剩下的棋盘使用弹珠填满，使得 $\operatorname{Alice}$ 无法再继续放置弹珠，因此 $\operatorname{Alice}$ 会输掉比赛。 第六组数据，$\operatorname{Alice}$ 可以选择在棋盘右上角斜线方向的中间两个空余位置放置 $2$ 颗弹珠，使得棋盘状态转化为样例输入的第五组数据，因此 $\operatorname{Alice}$ 会赢得比赛。 ------------ #### 数据范围 对于 $10\%$ 的数据，$0 \lt T \leq 10$。 对于 $60\%$ 的数据，$0 \lt T \leq 10^3$。 对于 $80\%$ 的数据，$0 \lt T \leq 10^5$。 对于 $100\%$ 的数据，$0 \lt T \leq 10^6$。 ------------ #### 提示 本题输入量较大，请使用合适的读入方式。