『JROI-2』Dancing Line
题目背景
> 若唤音乐随直线走动，那么你的双眸就是无穷。
k 舔喜欢玩 Dancing Line。
k 舔决定自己做一个 Dancing Line 关卡。
题目描述
注：本题不考虑「迷宫」等线转向方式特殊，「足球」等传送线，「钢琴」等飞跃落地的情况。
众所周知，Dancing Line 的路线是一条折线，每次点击会使线的前进方向**顺时针或逆时针旋转 $90^\circ$**，且**任意相邻两次旋转方向不同**。
比如下面是合法的路径（路径**不一定要随着平面直角坐标系的网格行走**）：
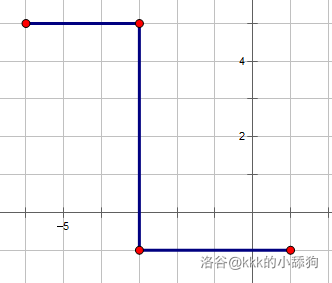
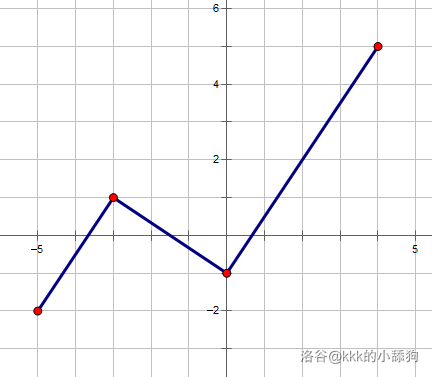
而下面是不合法的路径：
旋转角度不为 $90^\circ$：
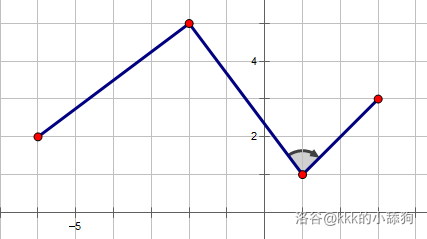
连续两次向左转弯：
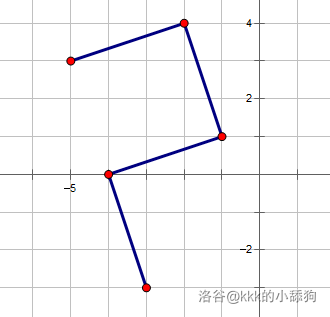
显然不符合要求的路径：
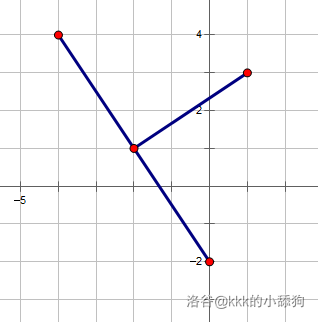
k 舔将路线放进了二维坐标系内，并记下了路线的**起点**、**终点**和**拐弯点**的坐标（横纵坐标**均为整数**），放进文件里就离开了。
等到 k 舔回来打开电脑时，发现他文件里的数据全部乱掉了，各点的坐标不再像之前那样按顺序存储好，而是按一种奇怪的顺序排列好了。
k 舔想要根据这些数据来重新复原这条路线，他还想要估计这个关卡的难度，用 $s$ 来表示：
$$s=\sum\limits_{i=1}^{n}{t_i^2},t_i=\dfrac{d(P_{i-1},P_i)}{v}$$
其中：
- $P_i(0\leq i\leq n)$ 表示路线**复原后**从起点开始的第 $i$ 个点（起点为 $P_0$，终点为 $P_n$）。
- $v$ 为线的速度，是一个给定的**正整数**。
- $d(A,B)$ 表示点 $A$ 和点 $B$ 在坐标轴内的距离。
你能帮助他吗？
输入输出格式
输入格式
第一行两个正整数 $n,v$，意义如上。
接下来 $n+1$ 行，每行两个整数，表示**复原前**文件内各点的坐标。
输出格式
一个数 $s$，意义如上，输出其对 $998244353$ 取模的结果。
具体来讲，设其用最简分数的方式表示为 $\dfrac{x}{y}$，你需要输出满足 $ys\equiv x\pmod{998244353}$ 的最小非负整数，在本题中你需要输出 $x\times y^{998244351}\bmod 998244353$。
输入输出样例
输入样例 #1
8 2
-7 7
-11 5
-3 4
-5 3
4 0
0 -2
5 -2
13 2
15 -2
输出样例 #1
249561142
说明
**样例解释**
对于样例一，路线如下：
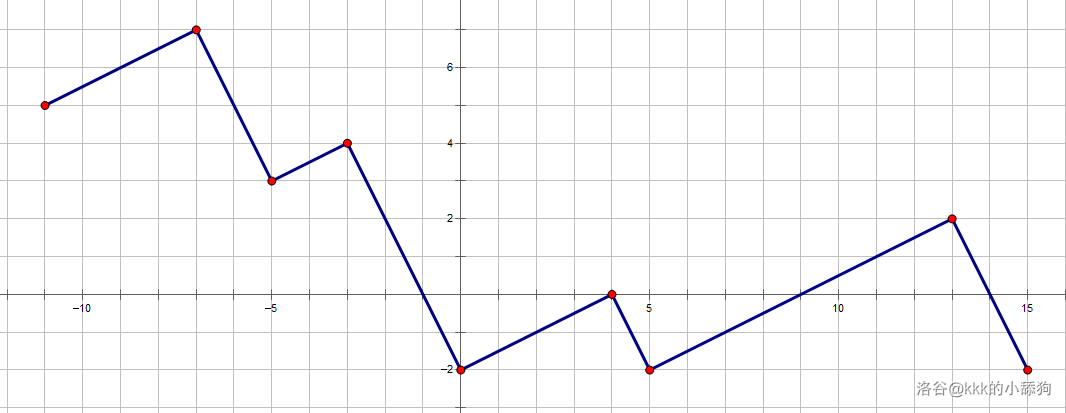
各段长度分别为 $2\sqrt{5},2\sqrt{5},\sqrt{5},3\sqrt{5},2\sqrt{5},\sqrt{5},4\sqrt{5},2\sqrt{5}$，$s$ 值为 $53\dfrac{3}{4}$，取模后结果为 $249561142$。
------------
**数据范围与约定**
本题采用**捆绑测试**。
- Subtask 1（5 pts）：$n\leq 6$。
- Subtask 2（15 pts）：$n\leq 80$。
- Subtask 3（30 pts）：$n\leq 800$。
- Subtask 4（50 pts）：无特殊限制。
对于 $100\%$ 的数据，满足：
- $2\leq n \leq 10^6$。
- $-10^9\leq x_i,y_i\leq 10^9$。
- $1\leq v\leq 10^7$。
- **保证所有点坐标各不相同**。
- **保证给出的点一定能且只能复原出唯一的路径。**
------------
$d(A,B)=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}$，其中 $A(x_A,y_A),B(x_B,y_B)$。
-----
Source：[JROI-2 Summer Fun Round](https://www.luogu.com.cn/contest/30241) - T3
Idea&Sol&Data：[kkk的小舔狗](/user/104581)
Std&Retest：[Tony2](/user/171288)