P7830 [CCO 2021] Through Another Maze Darkly

**警告：滥用本题评测将被封号！**

黑暗迷宫是一个树形结构，有 $n$ 个房间和 $n - 1$ 个走廊，房间编号 $1, 2, \cdots, n$。 黑暗迷宫里面漆黑一片，你看不见自己在哪里。为了辨别方向，每个房间有一个激光指示器，初始指向连接这个房间的某一个走廊。你重复执行如下策略行动： - 将当前房间的激光指示器按顺时针方向旋转到下一个走廊 - 沿着激光指示器指向的走廊走到另一个房间 你打算从编号为 $1$ 的房间开始，将这个策略重复执行 $k$ 次，想知道自己会到达哪个房间。你觉得这个问题太简单了，于是进行了 $q$ 次询问。每次询问是相互独立的，即激光指示器每次都会回到初始状态。

无

无

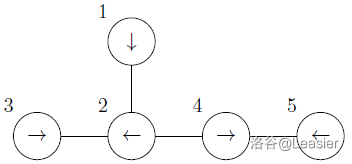
#### 样例 #1 解释 初始激光指示器的指向如图：  #### 数据范围 对于 $\frac{7}{45}$ 的数据，第 $i$ 个房间连接第 $i - 1$ 和第 $i + 1$ 个房间（如果这两个房间存在）； 对于另 $\frac{14}{45}$ 的数据，$2 \leq n \leq 2 \times 10^3$，$1 \leq q \leq 2 \times 10^3$； 对于另 $\frac{4}{15}$ 的数据，$q = 1$； 对于 $100\%$ 的数据，$2 \leq n \leq 8 \times 10^5$，$1 \leq q \leq 8 \times 10^5$，$1 \leq k \leq 10^{15}$，保证数据给出的是**一棵树**。 #### 题目来源 [CCO2021](https://cemc.math.uwaterloo.ca/contests/computing/2021/index.html) D1T3