「EVOI-RD2」旅行家

小 A 是一个热衷于旅行的旅行家。有一天，他来到了一个城市，这个城市由 $n$ 个景点与 $m$ 条连接这些景点的道路组成。每个景点有一个**美观度** $a_i$。 定义一条**旅游路径**为两个景点之间的一条非严格简单路径，也就是点可以重复经过，而边不可以。 接下来有 $q$ 个旅游季，每个旅游季中，小 A 将指定两个顶点 $x$ 和 $y$，然后他将走遍 $x$ 到 $y$ 的**所有旅游路径**。 所有旅游季结束后，小 A 会统计他所经过的所有景点的美观度之和（重复经过一个景点只统计一次美观度）。他希望你告诉他这个美观度之和。

第一行两个正整数 $n,m$。 第二行 $n$ 个正整数 $a_i$，代表顶点 $i$ 的权值。 接下来 $m$ 行，每行 $2$ 个正整数，表示一条无向边的两个端点。 然后一个正整数 $q$，代表有 $q$ 个旅游季。 接下来 $q$ 行，每行 $2$ 个整数 $x,y$，表示指定的起点和终点。

一行，一个整数表示最终的美观度总和。

5 5
1 2 3 4 5
1 2
2 3
1 4
4 3
3 5
3
1 2
1 4
1 3

10

5 6
1 2 3 4 5
1 2
2 3
1 4
1 5
4 3
3 5
3
1 2
1 4
1 3

15

**【数据规模与范围】** **本题采用捆绑测试** + Subtask 1 (30 pts)：$3 \leq n \leq 500,m \leq 2 \times 10^5,q=200$。 + Subtask 2 (30 pts)：$3 \leq n \leq 3 \times 10^5,m \leq 2 \times 10^6,q=10^6$。 + Subtask 3 (40 pts)：$3 \leq n \leq 5 \times 10^5,m \leq 2 \times 10^6,q=10^6$。 对于 $100\%$ 的数据，保证 $3 \leq n \leq 5 \times 10^5$，$m \leq 2 \times 10^6$，$q=10^6$，$1 \leq a_i \leq 100$，且该图联通，没有重边和自环。 --- **对于题面的解释：**  上图与样例无关。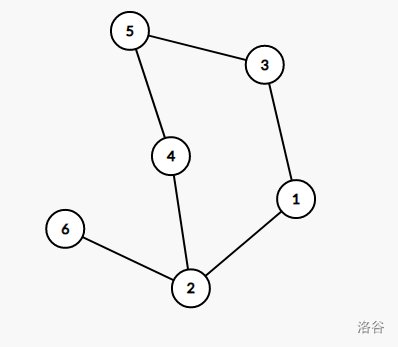 如图，为城市的景点分布图，为无向图。 假设 $6$ 号顶点为 $x$ 景点，$5$ 号顶点为 $y$ 景点。 很显然，路径 $6 \rightarrow 2 \rightarrow 4 \rightarrow 5$ 和路径 $6 \rightarrow 2 \rightarrow 1 \rightarrow 3 \rightarrow 5$ 都是合法的，这两条路径满足了都是简单路径的条件，并且都是在一次旅游季中行走的。 虽然 $6 \rightarrow 2$ 这条边经过了 $2$ 次，但仍旧是合法的，因为它们不是在一条路径中经过的。 简单来说，一次旅游季会走不定条路径，每条路径必须是简单路径，但是每条简单路径之间可以有重边。