Welcome to Lunatic City

M 国由 $n$ 个城市，$n-1$ 条双向高速铁路组成。其中的 $n$ 个城市可经过铁路互相抵达。 由于 M 国有着最顶尖的科技，为了加快交通速度，它可以在铁路上放置若干的互相配对的传送门，但总对数不超过 $L$。当一个列车在一条铁轨上运行时，每当它遇到一个传送门，就会进行传送。每个传送门分为正面与反面，列车从正面进入传送门时就会从与这个传送门配对的传送门的正面出来，从反面进入就从反面出来。传送门可以设立在一条铁路中间的任何地方。（如果对这一段描述有问题可以参考样例解释） 同时由于 M 国有着最高速的列车，列车的行驶时间仅消耗在停靠。于是从城市 $i$ 到城市 $j$ 的距离 $dis(i,j)$ 定义为列车所经过的城市数（包含终点但不包含起点）。 现在 M 国设立了 $m$ 个重要城市 $x_1,x_2,\dots,x_m$，请通过合理放置不超过 $L$ 对传送门使得 M 国的首都 $1$ 号城市到这些城市的距离和最小，即最小化 $\sum_{i=1}^mdis(1,x_i)$，并构造方案。同时放置的传送门必须保证城市间仍互相可达。 （由于 spj 的某些特性，请不要在一条铁路上放超过 $L$ 个传送门，否则会被判断为 WA）

第一行一个数 $T$ 表示数据组数。 接下来对于每一组数据： 第一行三个整数 $n$，$m$ 和 $L$ 表示城市数，$x$ 的长度和最多放置的传送门对数。 接下来 $n-1$ 行，第 $i$ 行两个正整数 $u_i,v_i$ 表示第 $i$ 条铁路连接的两个城市。 接下来一行 $m$ 个整数表示 $x$。

对于每组数据： 第一行一个整数表示最小距离和。 接下来 $n-1$ 行，第 $i$ 行开头一个整数 $num$ 表示第 $i$ 条铁路上的传送门数。然后 $num$ 对整数 $x,f$ 描述了从 $u_i$ 到 $v_i$ 传送门依次的编号与朝向，$f=0$ 表示正面朝向城市 $u_i$，$f=1$ 表示正面朝向城市 $v_i$。 传送门编号为 $1\sim \frac{\sum num}{2}$ 且每种编号必须恰好出现两次。 对于每组数据，传送门总对数不得超过 $L$，即 $\frac{\sum num}{2}\le L$。

2
4 3 100
1 2
2 3
3 4
2 3 4
5 2 100
1 2
2 3
3 4
3 5
4 5

6
0
0
0
5
1 1 0
3 4 0 3 1 1 1
1 2 0
3 2 1 3 0 4 1

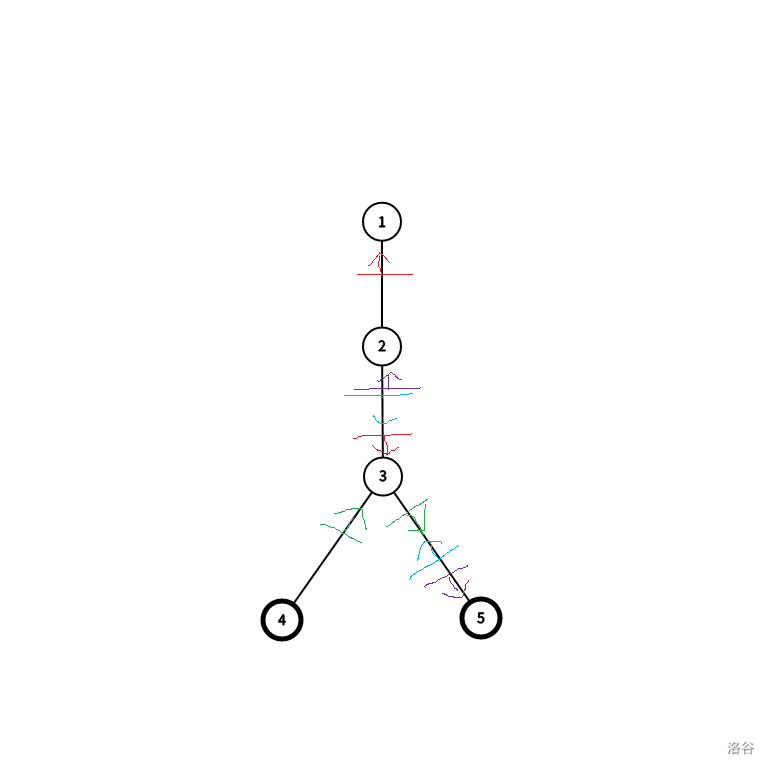
### 样例解释 对于样例的第二组数据，树的形态及传送门的放置方式如下：  其中红色门编号为 $1$，绿色编号为 $2$，蓝色编号为 $3$，紫色编号为 $4$。箭头表示传送门的正面所朝的方向。加粗的点表示重要城市。 其中 $1$ 号城市到 $5$ 号城市的最短路径如下：  首先由 $1$ 号城市出发，进入红色传送门的正面到达 $3$ 号城市。  随后从 $3$ 号城市出发，从绿色传送门的正面进入，到达 $3-5$ 这条路上绿色与蓝色传送门中间的一段铁路上，再从蓝色传送门正面进入，到达 $2-3$ 这条路中蓝色与红色传送门中间的一段铁路上，再由红色传送门的背面进入，最终到达 $2$ 号城市。  最后再从紫色传送门的正面进入，最终到达 $5$ 号城市。中途除去 $1$ 号城市分别经过了 $3,2,5$ 号城市，于是在这种传送门的放置方式下 $dis(1,5)=3$。 同时有 $dis(1,4)=2$，可以证明不存在让 $dis(1,4)+dis(1,5)$ 更小的放置方案。 ### 数据范围 **本题采用捆绑测试** | 子任务编号 | 分值 | 特殊限制 | | :----------: | :----------: | :----------: | | $0$ | $15$ | $n\le 9$，$L=100$ | | $1$ | $10$ | $m=n-1$，$L=5n$ | | $2$ | $20$ | $n\le 70$ 且 $n>30$ 的数据不超过五组，$L=n^2$ | | $3$ | $20$ | $n\le 1000$ 且 $n>100$ 的数据不超过五组，$L=100n$ | | $4$ | $30$ | $L=5n$ | | $5$ | $5$ | $L=n$ | 对于所有数据，保证 $1\le T\le 100$，$1\le n\le 10^5$，$1\le \sum n\le 5\times 10^5$，$0\le m<n$，$2\le x_i\le n$，$x_i$ 互不相同。