「MCOI-08」Fast Enumeration

Technoblade 将 Skyblock 抽象为一张 $n$（$n\le 50$）节点 $m$ 条边的简单有向图。他需要求出该图 **所有** 哈密尔顿回路，即所有排列 $p_1,p_2,\dots,p_n$ 使得 $p_1=1$ 并且 $p_1\to p_2\to \dots\to p_{n-1}\to p_n\to p_1$ 为一个合法路径。 **数据保证哈密尔顿回路数量非零并小于 $10^4$**。 **数据从所有合法数据随机采样。**

第一行两个正整数 $n,m$。 接下来 $m$ 行，每行两个正整数 $u,v$。

输出若干行；每行输出 $n$ 个正整数，为一个哈密尔顿回路。按照递增字典序输出。

3 3
1 2
2 3
3 1

1 2 3

4 6
1 3
1 4
2 1
2 3
3 4
4 2

1 3 4 2

5 8
1 2
2 3
3 4
4 1
2 5
4 5
5 1
5 3

1 2 3 4 5
1 2 5 3 4

5 10
1 2
1 3
2 3
2 4
3 4
3 5
4 1
4 5
5 1
5 2

1 2 3 4 5
1 3 5 2 4

6 15
1 3
1 4
1 5
2 1
2 3
2 4
3 1
3 4
4 2
4 6
5 2
5 3
6 1
6 2
6 3

1 5 2 3 4 6
1 5 2 4 6 3
1 5 3 4 6 2

6 15
1 3
1 5
2 1
2 4
3 1
3 2
3 4
3 5
3 6
4 6
5 1
5 4
5 6
6 3
6 5

1 3 2 4 6 5
1 5 4 6 3 2

6 16
1 3
1 6
2 3
2 4
2 6
3 1
3 6
4 2
4 3
4 5
4 6
5 2
5 6
6 1
6 3
6 5

1 6 5 2 4 3

6 21
1 2
1 5
1 6
2 1
2 3
2 4
2 5
3 1
3 2
3 4
3 6
4 1
4 2
4 6
5 1
5 2
5 4
5 6
6 2
6 3
6 4

1 2 5 4 6 3
1 2 5 6 3 4
1 5 2 3 6 4
1 5 2 4 6 3
1 5 4 6 2 3
1 5 4 6 3 2
1 5 6 2 3 4
1 5 6 3 2 4
1 5 6 3 4 2
1 5 6 4 2 3
1 6 3 2 5 4
1 6 3 4 2 5

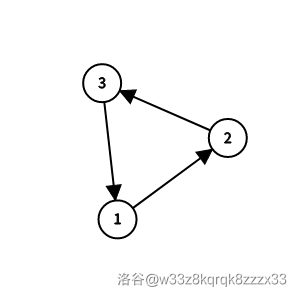
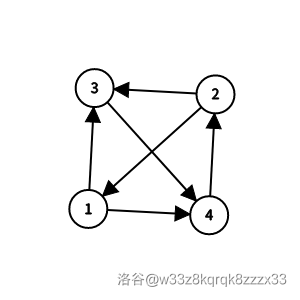
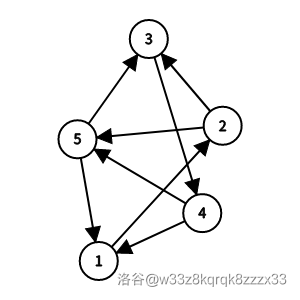
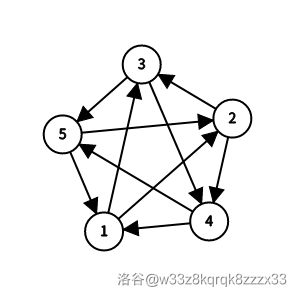
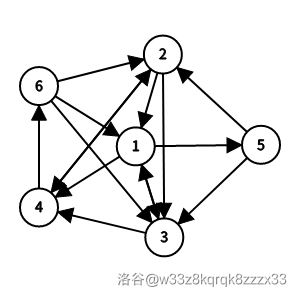
#### 样例 1 解释  有 $1$ 个哈密尔顿回路： - $1\to2\to3\to1$。 #### 样例 2 解释  有 $1$ 个哈密尔顿回路： - $1\to3\to4\to2\to1$。 #### 样例 3 解释  有 $2$ 个哈密尔顿回路： - $1\to2\to3\to4\to5\to1$； - $1\to2\to5\to3\to4\to1$。 #### 样例 4 解释  有 $2$ 个哈密尔顿回路： - $1\to2\to3\to4\to5\to1$； - $1\to3\to5\to2\to4\to1$。 #### 样例 5 解释  有 $3$ 个哈密尔顿回路： - $1\to5\to2\to3\to4\to6\to1$； - $1\to5\to2\to4\to6\to3\to1$； - $1\to5\to3\to4\to6\to2\to1$。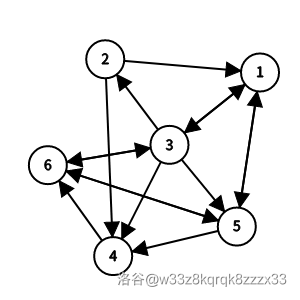 #### 样例 6 解释  有 $2$ 个哈密尔顿回路： - $1\to3\to2\to4\to6\to5\to1$； - $1\to5\to4\to6\to3\to2\to1$。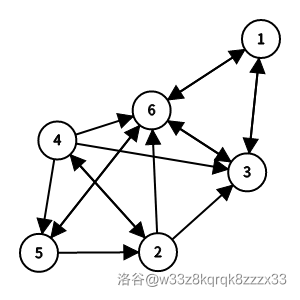 #### 样例 7 解释  有 $1$ 个哈密尔顿回路： - $1\to6\to5\to2\to4\to3\to1$。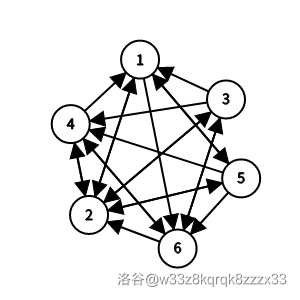 #### 样例 8 解释  有 $12$ 个哈密尔顿回路： - $1\to2\to5\to4\to6\to3\to1$； - $1\to2\to5\to6\to3\to4\to1$； - $1\to5\to2\to3\to6\to4\to1$； - $1\to5\to2\to4\to6\to3\to1$； - $1\to5\to4\to6\to2\to3\to1$； - $1\to5\to4\to6\to3\to2\to1$； - $1\to5\to6\to2\to3\to4\to1$； - $1\to5\to6\to3\to2\to4\to1$； - $1\to5\to6\to3\to4\to2\to1$； - $1\to5\to6\to4\to2\to3\to1$； - $1\to6\to3\to2\to5\to4\to1$； - $1\to6\to3\to4\to2\to5\to1$。 #### 数据规模与约定 对于固定 $n$ 和 $P$，任意一张 $m$ 条边的图权重为 $\left(\frac{1}{P}\right)^m\left(\frac{P-1}{P}\right)^{n^2-n-m}$。 - Subtask 1（1 pts）：为样例。 - Subtask 2（16 pts）：$n=15$。 - Subtask 3（20 pts）：$n=30$。 - Subtask 4（26 pts）：$n=40$。 - Subtask 5（37 pts）：$n=50$。