「MCOI-08 / AC6-M12」Weapons of Mass Destruction

Garuda Team, I've got some good news. The chemical agent used as a catalyst for their WMD is being transported to our shores from the Estovakian mainland. This catalyst has already been carried into the outskirts of Gracemeria. As a measure of caution against any attempts to destroy it, it has been concealed at Fort Norton in Gracemeria's north. If we start advancing again, the enemy will most likely bring the catalyst into Gracemeria at a faster pace. If in fact weapons of mass destruction are used on the population of Gracemeria, the resulting devastation can't be expressed in enough words. It will lead to unspeakable tragedies. We've used this intelligence to come up with a solid proposal on how to prevent this scorched earth policy from being executed in our capital. Just a minute ago, we received a letter of approval for our prevention plan from the Joint Chiefs of Staff. The proposal we put on the table for our scorched earth prevention policy is really quite simple. While the enemy transport unit is stationed at Fort Norton, **we'll ambush them.** We like to call it our tactic for pre-emptive victory. The enemy has loaded this catalyst into their transport vehicles and is able to send them into Gracemeria at any time. This plan will be carried out by a handful of our top pilots under absolute secrecy. **Fly through Fort Norton's canyon at an extremely low altitude to avoid radar detection, and take out those transport vehicles.** We've determined that a high-risk mission of this magnitude could not be executed by anyone other than Garuda Team. We're counting on a flawless execution here. $$_{{\frac{\large\text{ACE COMBAT }\Large6}{\tiny{\text{F i r e s\quad O f\quad L i b e r a t i o n}}}}}\\ \text{Mission 12} \\\Large\text{Weapons of Mass Destruction}\\\tiny -\textit{ Boiling Point }-$$ 

为了摧毁敌方装载有 WMD 催化剂的车队，你需要在超低空穿过 Fort Norton 的峡谷以接近他们。 Fort Norton 抽象为**平面上两个关于 $y$（$y\in[0,10^7]$）的线性分段函数** $A(y):y\mapsto x$ 以及 $B(y):y\mapsto x$，其中对于任意实数 $y\in [0,10^7]$，**满足 $A(y) \le B(y)$**。 你和你的 F-15E 抽象为一质点，**初始位置是 $(X_1,0)$**，保证 $A(0)\leq X_1\leq B(0)$；**同时具有初速度 $(v_0,\theta_0)$，表示初速的大小和方向**。 为了避免敌方发现，你不能大功率开动发动机。你的动力刚好足够在保持平飞的时候保持匀速。 当然你可以转向。由于你是 Ace Combat 的主角，你的转向全部用 PSM 完成。具体来说，你的飞行轨迹应为一条由若干线段组成的折线。但是在转向中会受到阻力。**如果方向改变后的角与改变前的角的差的绝对值为 $\alpha$，则速度大小会减小 $\alpha$**。如果你不改变方向，那么你会一直做匀速直线运动。 由于 Ghost Eye 很着急完成任务，所以**你的 $y$ 坐标必须随时间递增**。 同时，你需要保证在任意时刻，你所在的位置 $(x,y)$ 满足 $A(y)\le x\le B(y)$。 PSM 转向的过载很大，因此你需要保证**转向次数不超过 $\bf 3\times 10^6$**。~~否则你就会像 Prez 一样 g-LOC 并一头栽在仪表盘上。~~ 求任何一个转向方案，使得你运动到 $(X_2,10^7)$ 上（**即，速度不能在运动过程中变为 $\bf0$ 或负数**），同时转向次数不超过 $3\times 10^6$。类似的，保证 $A(10^7)\leq X_2\leq B(10^7)$。

第一行四个整数 $n,m,X_1,X_2$ 和两个实数 $v_0,\theta_0$。 **保证 $v_0\pm 10^{-6}$ 范围内解存在性不变。** 接下来 $n$ 行，每行两个整数 $x,y$，保证 $y$ 递增，第一个 $y$ 是 $0$，最后一个 $y$ 是 $10^7$。把这些点依次用线段连接起来即得到函数 $A$。 接下来 $m$ 行，每行两个整数 $p,q$ 表示函数 $B$，与 $A$ 的输入方式同理。

先输出一行 `1`。 然后由于这个点的运动轨迹一定是一条折线，所以你需要在下一行输出端点数 $K$；接下来输出 $K$ 行，每行两个实数表示这个端点的坐标。假设你给出的点列是 $C:\{(s_1,t_1),(s_2,t_2),\cdots,(s_K,t_K)\}$，那么表示 $\forall i\in [1,K)$，$C_iC_{i+1}$ 之间连线，得到的折线就是你给出的运动轨迹。 你需要保证： - $C_1$ 与 $X_1$ 重合，$C_K$ 与 $X_2$ 重合； - **$C$ 中 $y$ 坐标单调；** - 对于任意 $1\leq i<K$，有 $t_i<t_{i+1}$； - 对于任意折线上的点 $(x,y)$，满足 $A(y)-10^{-6}\leq x\leq B(y)+10^{-6}$； - 运动过程中速度大于 $0$； - $K\leq 3\times10^6$。 如果你正确输出了一种符合上述要求的方案，即被判为 Accepted。否则判为 Wrong Answer。如果有不止一种方案，输出任意一种皆可。 **本题开启 Special Judge。**

5 4 4000000 9000000 13 0
3000000 0
1000000 1000000
2000000 4000000
6000000 8000000
7000000 10000000
5000000 0
4000000 2000000
6000000 6000000
10000000 10000000

1
4
4000000.0000000000 0.0000000000
3000000.0000000000 2000000.0000000000
4000000.0000000000 6000000.0000000000
9000000.0000000000 10000000.0000000000

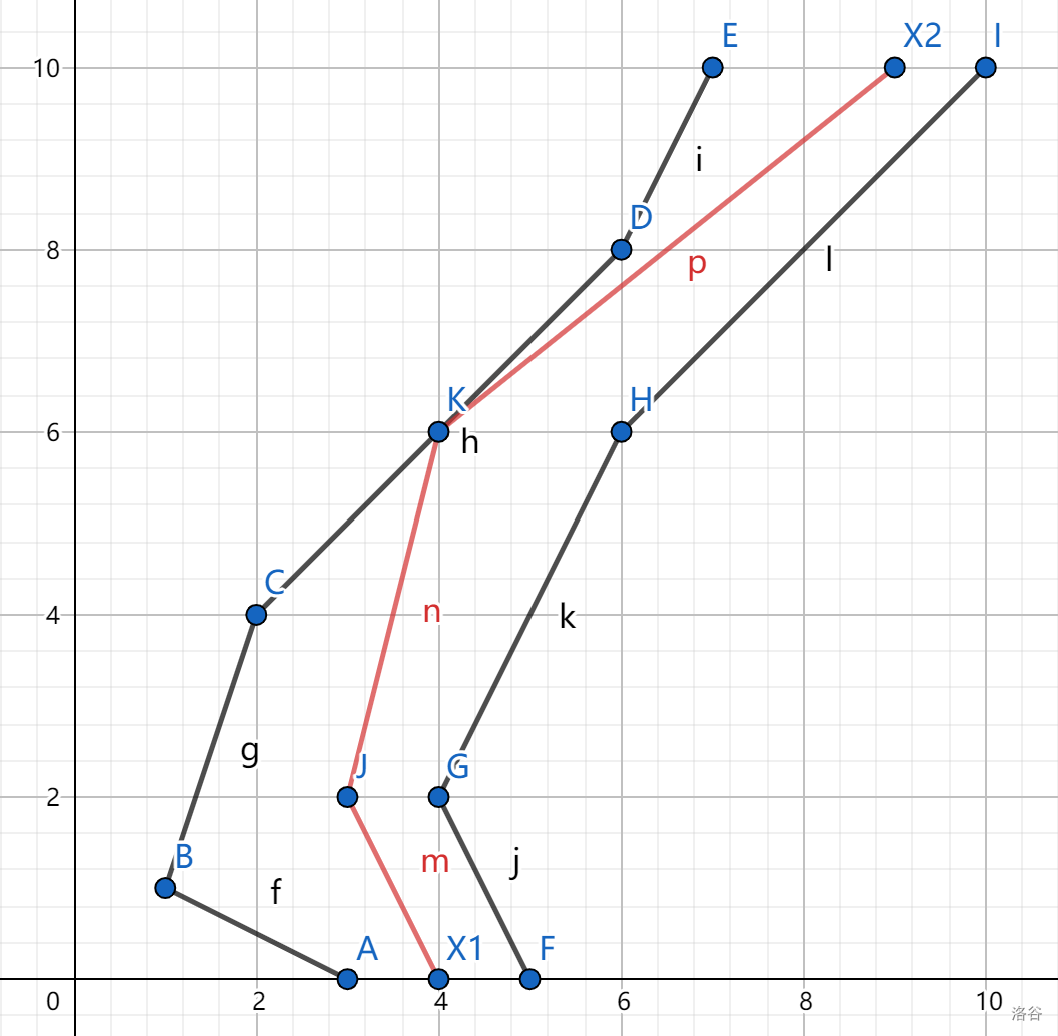
样例解释（缩小 $10^6$ 倍）：  **注意质点在运动过程中可以碰到边界，也可以沿着边界运动一段。** --- 对于 $100\%$ 的数据，保证 $2\leq n,m\leq 10^6$，$0\leq x,y,p,q\leq 10^7$，$x_1\leq X_1\leq p_1$，$x_n\leq X_2\leq p_m$，$0\leq \theta_0<\pi$，$0\leq v_0\leq 10^9$。 对于 $100\%$ 的数据，实数精度不超过 $12$ 位。 对于 $100\%$ 的数据，**保 证 有 解**。 - Subtask 1（3 pts）：$n,m\leq 6$；$v_0\ge 50$。 - Subtask 2（8 pts）：$n,m\leq 6$。 - Subtask 3（17 pts）：$n,m\leq 200$。 - Subtask 4（13 pts）：$n,m\leq 1500$。 - Subtask 5（17 pts）：$n,m\leq 5000$。 - Subtask 6（19 pts）：$n,m\leq 10^5$。 - Subtask 7（23 pts）：无特殊限制。 **请注意浮点数输出效率。** --- idea：Sol1，solution：Sol1 & w33z8kqrqk8zzzx33，code：Sol1，data：w33z8kqrqk8zzzx33